Assessment of centennial (1918–2019) drought features in the Campania region by historical in situ measurements (southern Italy)

Drought is a sustained period of below-normal water availability. It is a recurring and worldwide phenomenon, but the Mediterranean Basin is seen as a very vulnerable environment in this perspective, and understanding historical drought conditions in this area is necessary to plan mitigation strategies to further face future climate change impacts. The current research was aimed at the description of drought conditions and evolution for the Campania region (southern Italy), assessed by the analysis of an in situ measurement database which covers a centennial period from 1918 to 2019. Standardized Precipitation Index (SPI) time series were reconstructed for different accumulation timescales (from 3 to 48 months) and the modified Mann–Kendall and Sen's tests were applied to identify SPI changes over time. SPI time series were mostly affected by a negative trend, significant for a very large area of the region, particularly evident for the accumulation scales longer than 12 months. Mean drought duration (MDD), severity (MDS) and peak (MDP) were furthermore investigated for both moderate (SPI ≤ −1) and extremely severe conditions (SPI ≤ −2). The accumulation scale affected the drought features, with longer duration and larger severity associated with the larger accumulation scales. Drought characteristics spatial patterns were not congruent for the different SPI timescales: if duration and severity were larger in the southern areas, peaks appeared mostly severe in the northern areas of the region. Extremely severe events were featured by shorter durations and larger severity compared to the moderate drought events but were very less frequent (over 75 % less then) and did not appear to be focused on specific areas of the region.

1 Introduction

Drought is a natural local or regional disaster which affects agricultural, hydrological and socioeconomic groundwater systems (Dracup et al., 1980; Mishra and Singh, 2010; Wilhite and Glantz, 1985). Climate change is likely to accelerate the climate–meteorological–hydrological processes able to lead to intense drought episodes in specific environments (Longobardi and Van Loon, 2018), and, in this perspective, in recent years and in several world regions, the evolution of drought has been widely discussed and analyzed.

In different areas of Asia, the spatiotemporal variability of drought has been discussed by Zhang and Zhou (2015) and by Hasegawa et al. (2016). In America, regional drought events have been reviewed by Swain and Hayhoe (2015), Littell et al. (2016), and Sobral et al. (2019). Spinoni et al. (2015) and Stagge et al. (2017) analyzed drought events in different regions of Europe. In particular for this specific geographical context, according to the Intergovernmental Panel on Climate Change (IPCC) Fifth Assessment Report (AR5), the Mediterranean Basin is seen as a very vulnerable environment (IPCC, 2014), and a number of regional-scale drought analyses have indeed been performed in different regions of this area (Cook et al., 2016; Gouveia et al., 2017; Ruffault et al., 2018; Caloiero et al., 2019; Yves et al., 2020). At the global scale, south America, the Sahel, the Congo River Basin and northeastern China, besides the Mediterranean Basin, were the areas the most frequently affected by severe droughts (Spinoni et al., 2019).

The Italian territory is vulnerable to drought episodes, and unfortunately the temporal consistency and the spatial resolution of available data by rain gauge stations are frequently inadequate for drought characterization analysis. Beyond ground rainfall observations, data from global weather datasets can be considered, but their coarse spatial resolution makes them poorly effective especially in capturing the high precipitation variability that affects the southern European region. In this context, historical in situ long-term measurements are crucial for understanding historical drought conditions as they allow us to learn about how a specific region has been affected by precipitation shortage periods in the past, how severe the response was and how quickly it took to recover from drought conditions (Bonaccorso and Aronica, 2016; Marini et al., 2019). This information is important to set drought forecasting strategies which could help in preparedness actions, planning mitigation and adaptation strategies to projected climate change (Peres et al., 2020; Gaitán et al., 2020).

One of the widely used approach to define drought conditions and persistence consists in the use of mathematical indices, known as drought indicators, such as the Palmer Drought Severity Index (PDSI) (Palmer, 1965), the Crop Moisture Index (CMI) (Palmer, 1968), the Normalized Difference Vegetation Index (NDVI) (Rouse et al., 1974), the Standardized Precipitation Index (SPI) (McKee et al., 1993; Ganguli and Reddy, 2014), the Drought Recognition Index (RDI) (Tsakiris and Vangelis, 2005) and the Standardized Precipitation Evapotranspiration Index (SPEI) (Vicente-Serrano et al., 2010). In particular the SPI, despite the inherent limitations, was used in several studies to investigate drought characteristics across the world (Mishra and Singh, 2010; Van Loon, 2015).

Concerning the Italian territory, Capra et and Scicolone (2012) investigated the spatiotemporal variability of drought at short and medium accumulation scales in the Calabria region, southern Italy, using the SPI index, concluding that approximately half of the region was impacted by drought during the period 1981–1990 when the region suffered its worst drought. Di Lena et al. (2014) analyzed drought periods in the Abruzzo region, showing a general downward trend in SPI time series which were more pronounced on longer accumulation timescales. Marini et al. (2019) investigated droughts in the Apulia region using the SPI and the RDI indices, finding an upward trend in the severity of droughts in the western part and a downward trend in the eastern region. By applying the SPI index over 3 and 6 months for a short-term analysis and 12 and 24 months for a long-term analysis, Caloiero et al. (2018) analyzed dry and wet periods in southern Italy, showing that when long-term precipitation scales are included, the probabilities of occurrence of dry conditions are higher than the wet ones.

The reported case study is represented by the Campania region, located in southern Italy, which is a large area of about 13 600 km² stretching from the Apennine Mountains to the Mediterranean Sea with progressively decreasing elevations moving from the inland to the coastline. The climate regime of the study area is typically seasonal with some evident differences depending on the location (Longobardi and Villani, 2010; Longobardi and Mautone, 2015; Longobardi et al., 2016; Longobardi and Boulariah, 2021). Two distinct rain gauge networks are available for the region: one for the period 1918–1999 and the other for the period 2000–2019. They are characterized by different stations' consistency, localization and typology. With the aim of reconstructing continuous long-term monthly scale precipitation time series, the in situ point measurements (observed at the rain gauge locations) for the two datasets were projected on a 10×10 km resolution grid covering the whole region by using a geostatistical interpolation approach (Boulariah et al., 2020). Projecting the two distinct database point measurements to a common grid made it possible to reconstruct centennial monthly precipitation time series from 1918 to 2019, which is crucial for long-term historical drought condition analysis.

The reconstructed gridded precipitation database was used to compute the Standardized Precipitation Index at different accumulation time steps, from SPI_3 to SPI_48, to explore the full range of drought definitions. SPI time series were analyzed for their spatial and temporal patterns features, and the modified Mann–Kendall and the Sen's slope tests were used to assess the trend significance and magnitude. Additionally, the spatial patterns of drought characteristics were evaluated with the assessment of probability of occurrence, drought duration, drought severity and drought peak value for different SPI thresholds, according to the run theory (Yevjevich, 1967).

The findings of the study in terms of detailed spatial and temporal characterization of drought conditions within the Campania region represent essential information for sustainable and efficient water resource management planning strategies.

2 Material and methods

2.1 Study area

The Campania region is located between 40.0 and 41.5^∘ N and 13.5 and 16.0^∘ E, covering about 13 600 km² in the southwest of Italy (Fig. 1).

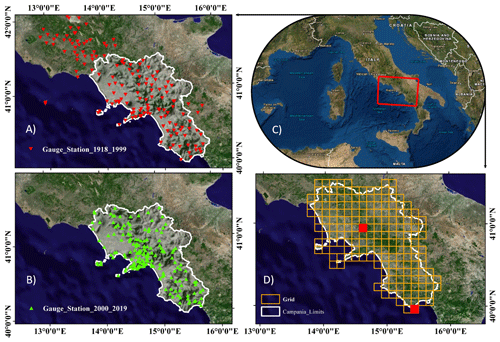
Figure 1 The studied area. (a, b) The two rain gauge networks. (c) The study area in the red box. (d) The grid shape for the region under investigation. Red boxes represent grid cells no. 2 and no. 108 reported in Fig. 3.

The region is well known for a complex orography; the altitude of the region ranges from well above 2000 m a.s.l. (above sea level) in the Apennine Mountains to the coastline. The region is characterized by a complex climatic pattern because of the orography. The seasonality is well defined, with the larger amount of precipitation recorded during the winter periods. The mean annual rainfall of the study area ranges from 600 to 2400 mm, whereas the average annual temperature is around 17 ^∘C. Trends in historical precipitation and their seasonal variability were described in Longobardi and Villani (2010) and Longobardi et al. (2016). The area is experiencing a moderate negative trend in precipitation, especially concerning the northeastern and southwestern areas. At the same time, the seasonal variability also appeared to be featured by a negative trend, with a transition of the precipitation regime from a seasonal to more uniform one.

2.2 Dataset

As mentioned in the introduction, the gridded datasets used in the current paper were obtained from the research carried out by Boulariah et al. (2020), in which different spatial interpolation approaches (both deterministic and geostatistical approaches) were applied to merge two monthly precipitation rain gauge (point) databases available for the studied region; they are different in rain gauge locations and moreover cover different periods of time, one referring to the period 1918–1999 and the second to 2000–2019 (Fig. 1a and b). The number of available rain gauge stations were 154 and 187 respectively for the first period and the second period. Comparing the two considered periods of time, rain gauge density is then rather similar and rain gauge stations are similarly distributed over the region, with an exception for the Sorrento Peninsula, a coastline area at the middle latitudes of the region. The two-point dataset (rain gauge dataset) were spatially interpolated by the co-kriging, which was found to be the best interpolating method over the investigated area based on the results of an interpolation approach comparative study, due to the high correlation (≥ 70 %) between elevation and observed precipitation (Boulariah et al., 2020). The interpolated precipitation fields (for each month and for each year) were projected on a high-resolution grid base (10×10 km). The result of the merging process was monthly gridded rainfall data from 1918 to 2019 for 191 high-resolution grid points covering the whole of the Campania region, which were considered for the proposed analysis (Fig. 1c).

2.3 The Standardized Precipitation Index

The formulation of the SPI drought index for any given location is based on the cumulative rainfall record over a selected timescale and the probability density function “Gamma”, which fit only positive and null values (McKee et al., 1993; Husak et al., 2007). In the literature and according to previous studies, the rainfall time series are first fitted to the Gamma distribution and then standardized by transformation into a normal distribution (Caloiero et al., 2018; Martinez et al., 2019; Stagge et al., 2015; Zhou and Liu, 2016). The probability density function for the Gamma distribution can be expressed by the following equation:

$$\begin{array}{}\text{(1)}& g\left(x\right)={\displaystyle \frac{\mathrm{1}}{{\mathit{\beta }}^{\mathit{\alpha }}\mathrm{\Gamma }\left(\mathit{\alpha }\right)}}{x}^{\mathit{\alpha }-\mathrm{1}}{e}^{-x/\mathit{\beta }},\end{array}$$

where α, β and x are respectively the shape parameter, the scale parameter and the amount of precipitation (α, β and x > 0). Γ(α) is the gamma function expressed as follows:

$$\begin{array}{}\text{(2)}& \mathrm{\Gamma }\left(\mathit{\alpha }\right)={\int }_{\mathrm{0}}^{\mathrm{\infty }}{y}^{\mathit{\alpha }-\mathrm{1}}{e}^{-y}\mathrm{d}y.\end{array}$$

Parameters $\widehat{\mathit{\alpha }}$ and $\widehat{\mathit{\beta }}$ are assessed through the maximum likelihood method (McKee et al., 1993; Liu et al., 2016):

$$\begin{array}{}\text{(3)}& \widehat{\mathit{\alpha }}={\displaystyle \frac{\mathrm{1}}{\mathrm{4}A}}\left(\mathrm{1}+\sqrt{\mathrm{1}+{\displaystyle \frac{\mathrm{4}A}{\mathrm{3}}}}\right)\mathrm{and}\widehat{\mathit{\beta }}={\displaystyle \frac{\stackrel{\mathrm{‾}}{x}}{\widehat{\mathit{\alpha }}}},\end{array}$$

where

$$\begin{array}{}\text{(4)}& A=\ln \left(\stackrel{\mathrm{‾}}{x}\right)-{\displaystyle \frac{\sum \ln \left(x\right)}{n}}\end{array}$$

for n observations. By integrating the density of probability function g(x), the cumulative probability G(x) is obtained:

$$\begin{array}{}\text{(5)}& G\left(x\right)=\underset{\mathrm{0}}{\overset{x}{\int }}g\left(x\right)\mathrm{d}x={\displaystyle \frac{\mathrm{1}}{\widehat{\mathit{\beta }}\mathrm{\Gamma }\left(\widehat{\mathit{\alpha }}\right)}}=\underset{\mathrm{0}}{\overset{x}{\int }}{x}^{\widehat{\mathit{\alpha }}-\mathrm{1}}{e}^{-\frac{x}{\mathit{\beta }}}\mathrm{d}x.\end{array}$$

Given that the Gamma distribution is not defined for x values equal to zero and that instead the cumulative rainfall series may contain null values, the cumulative distribution is re-defined as follows:

$$\begin{array}{}\text{(6)}& H\left(x\right)=q+(\mathrm{1}-q)G\left(x\right),\end{array}$$

where q is the probability of zero precipitation. Then, the value of the SPI can be obtained through the approximation proposed in Abramowitz and Stegun (1964) which converts the cumulative distribution H(x) to a normal random variable Z:

$$\begin{array}{}\text{(7)}& {\displaystyle }\begin{array}{rl}Z& =\mathrm{SPI}\\ & =\left\{\begin{array}{cc}-\left(t-\frac{c_{\mathrm{0}}+c_{\mathrm{1}}t+c_{\mathrm{2}}{t}^{\mathrm{2}}}{\mathrm{1}+d_{\mathrm{1}}t+d_{\mathrm{2}}{t}^{\mathrm{2}}+d_{\mathrm{3}}{t}^{\mathrm{3}}}\right),& \mathrm{for}\mathrm{0}<H\left(x\right)\le \mathrm{0.5}\\ +\left(t-\frac{c_{\mathrm{0}}+c_{\mathrm{1}}t+c_{\mathrm{2}}{t}^{\mathrm{2}}}{\mathrm{1}+d_{\mathrm{1}}t+d_{\mathrm{2}}{t}^{\mathrm{2}}+d_{\mathrm{3}}{t}^{\mathrm{3}}}\right),& \mathrm{for}\mathrm{0.5}<H\left(x\right)\le \mathrm{1}\end{array}\right.,\end{array}\text{(8)}& {\displaystyle }t=\left\{\begin{array}{cc}\sqrt{\ln \left[\frac{\mathrm{1}}{\left(H\right(x){)}^{\mathrm{2}}}\right]},& \mathrm{for}\mathrm{0}<H\left(x\right)\le \mathrm{0.5}\\ \sqrt{\ln \left[\frac{\mathrm{1}}{(\mathrm{1}-H(x){)}^{\mathrm{2}}}\right]},& \mathrm{for}\mathrm{0.5}<H\left(x\right)\le \mathrm{1}\end{array}\right.,\end{array}$$

where

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{c}_{\mathrm{0}}=\mathrm{2.515517},c_{\mathrm{1}}=\mathrm{0.802853},c_{\mathrm{2}}=\mathrm{0.010328},\\ {\displaystyle }& {\displaystyle }{d}_{\mathrm{0}}=\mathrm{1.432788},d_{\mathrm{1}}=\mathrm{0.189269},d_{\mathrm{2}}=\mathrm{0.001308}.\end{array}$$

SPI time series for different accumulation periods of 3, 6, 12, 24, 36 and 48 months (respectively SPI_3, SPI_6, SPI_12, SPI_24, SPI_36 and SPI_48) were computed for the studied dataset and used to describe wet and dry conditions according to the values reported in Table 1 (McKee et al., 1993).

Table 1 Classification of wet and dry conditions according to SPI values (McKee et al., 1993).

2.4 Trend analysis

Time series of SPI were tested for trend detection in time. A trend is a significant change over time exhibited by a random variable, detectable by statistical parametric and non-parametric procedures. Provided the intrinsic autocorrelation of the analyzed time series, the current study provided results for non-parametric modified Mann–Kendall (MMK) and Sen's test approaches. Those methods are briefly described in the following.

The Mann–Kendall test (Mann, 1945; Kendall, 1962) is one of the most widely used methods to detect trend in climatology analysis. It is used to analyze data collected over time for consistently increasing or decreasing trends (monotonic). It is a non-parametric test, which means it works for all distributions; thus tested data do not have to meet the assumption of normality but should have no serial correlation. The Mann–Kendall statistic S is defined as follows:

$$\begin{array}{}\text{(9)}& S=\sum _{i=\mathrm{1}}^{n-\mathrm{1}}\sum _{j=i+\mathrm{1}}^n\mathrm{sign}(x_j-x_i),\end{array}$$

where

$$\begin{array}{}\text{(10)}& \begin{array}{l}\mathrm{sign}(x_j-x_i)=\left\{\begin{array}{l}+\mathrm{1},\mathrm{if}(x_j-x_i)>\mathrm{1}\\ \mathrm{0},\mathrm{if}(x_j-x_i)=\mathrm{0}\\ -\mathrm{1},\mathrm{if}(x_j-x_i)<\mathrm{1}\end{array}\right\},\end{array}\end{array}$$

where x_i and x_j are the annual values in years i and j, with i > j. When n ≥ 10, the statistic S is almost normally distributed with mean E(S) and variance Var(S) as follows:

$$\begin{array}{}\text{(11)}& E\left(S\right)=\mathrm{0},\mathrm{Var}\left(S\right)={\displaystyle \frac{n(n-\mathrm{1})(\mathrm{2}n+\mathrm{5})}{\mathrm{18}}}.\end{array}$$

However, the expression of Var(S) should be adjusted when tied values do exist:

$$\begin{array}{}\text{(12)}& \mathrm{Var}\left(S\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{18}}}\left[n(n-\mathrm{1})(\mathrm{2}n+\mathrm{5})-\sum _{p=\mathrm{1}}^q{t}_p(t_p-\mathrm{1})(\mathrm{2}{t}_p+\mathrm{5})\right],\end{array}$$

where q is the number of tied groups and t_p is the number of data values in the pth group. The standardized test statistic Z follows a standard normal distribution and is computed as follows:

$$\begin{array}{}\text{(13)}& Z=\left\{\begin{array}{ll}\frac{S-\mathrm{1}}{\sqrt{\mathrm{Var}\left(S\right)}}& \mathrm{if}S>\mathrm{0}\\ \mathrm{0}& \mathrm{if}S=\mathrm{0}\\ \frac{S+\mathrm{1}}{\sqrt{\mathrm{Var}\left(S\right)}}& \mathrm{if}S<\mathrm{0}\end{array}\right\}.\end{array}$$

At the significance level α, the existing trend is considered to be statistically significant if $p\le \mathit{\alpha }/\mathrm{2}$ in the case of the two-tailed test.

To take into account the presence of autocorrelation in the SPI time series, which might increase the probability to detect trends when actually none exist, the modified Mann–Kendall test can be applied (Hamed and Rao, 1998). Furthermore, the reason for the use the modified Mann–Kendall test (MMK) lays in its accuracy for the analysis of correlated data (Hamed and Rao, 1998; Mondal et al., 2012; Sa'adi et al., 2019), which is the case for the SPI time series in this study, compared to the original Mann–Kendall trend test without any loss of power. For this purpose, a modified form of Var(S), set as Var(S)^*, is used as follows:

$$\begin{array}{}\text{(14)}& \mathrm{Var}{\left(S\right)}^{*}=\mathrm{Var}\left(S\right){\displaystyle \frac{n}{n^{*}}},\end{array}$$

where n^* is the effective sample size and n the number of observations. The ratio between the effective sample size and the actual number of observations was computed as proposed by Hamed and Rao (1998) as follows:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{\displaystyle \frac{n}{n^{*}}}& =\mathrm{1}+{\displaystyle \frac{\mathrm{2}}{n(n-\mathrm{1})(n-\mathrm{2})}}\sum _{i=\mathrm{1}}^{n-\mathrm{1}}\\ & (n-i)(n-i-\mathrm{1})(n-i-\mathrm{2})r_i,\end{array}\end{array}$$

where r_i is the lag-i significant auto-correlation coefficient of rank i of the time series.

Sen (1968) developed a non-parametric procedure to assess the slope of trend in a sample of N pairs of data:

$$\begin{array}{}\text{(16)}& Q_i={\displaystyle \frac{x_j-x_i}{j-i}},i=\mathrm{1},\mathrm{2},\mathrm{\dots }Nj>i,\end{array}$$

where x_j and x_i are data values at time j and i (j > i) respectively. If there is only one datum in each time period, then $N=n(n-\mathrm{1})/\mathrm{2}$, where n is the number of time periods. If there are multiple observations in one or more time periods, then $N=n(n-\mathrm{1})/\mathrm{2}$, where n is the total number of observations.

The N values of Q_i are ranked from smallest to largest, and the median of slope or Sen's slope estimator is computed as

$$\begin{array}{}\text{(17)}& Q_{\mathrm{med}}=\left\{\begin{array}{ll}{Q}_{\frac{N+\mathrm{1}}{\mathrm{2}}}& \mathrm{if}N\mathrm{is}\mathrm{odd}\\ \frac{\mathrm{1}}{\mathrm{2}}\left[Q_{\frac{N}{\mathrm{2}}}+Q_{\frac{N+\mathrm{2}}{\mathrm{2}}}\right]& \mathrm{if}N\mathrm{is}\mathrm{even}\end{array}\right\}.\end{array}$$

The Q_med sign reflects the data trend behavior (increase or decrease), while its value indicates the steepness of the trend.

2.5 Drought characteristics

To describe meteorological drought features of the studied area, the occurrence of drought events was evaluated for each cell of the gridded dataset according to the SPI threshold, and the average over the period of observation was illustrated. Two different thresholds in the SPI value were used, SPI $\le -\mathrm{1}$ and SPI $\le -\mathrm{2}$, to detect the behavior of the region with respect to moderate and extremely severe drought conditions (see Table 1). The effect of the accumulation period was investigated.

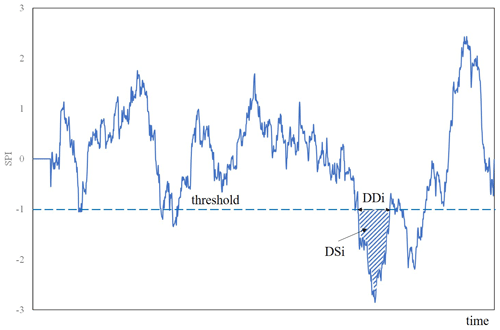
Additionally, three drought characteristics, namely mean drought duration (MDD), mean drought severity (MDS) and mean drought intensity (MDP) (Guo et al., 2018; Wang et al., 2019; Fung et al., 2020), were selected. By linking the SPI data with the “run theory” proposed by Yevjevich (1967) and according to Wang et al. (2019), MDD and MDS were calculated as follows:

$$\begin{array}{}\text{(18)}& {\displaystyle }\mathrm{MDD}={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^N{\mathrm{DD}}_i}{N}},\text{(19)}& {\displaystyle }\mathrm{MDS}={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^N{\mathrm{DS}}_i}{N}},{\mathrm{DS}}_i={\sum }_{{\mathrm{DD}}_i}\mathrm{SPI},\end{array}$$

where, provided a given SPI threshold, DD is the period of time with continuous (negative) values of the SPI below the given threshold (i.e. drought spell duration in the run theory), i is the number of the sequence of DD, N is the total number of drought spells observed during the studied period, and DS_i is the value of drought severity associated with the period DD_i (Fig. 2). Events with DD ≥ 3 months were only accounted for. Additionally, the mean drought intensity MDP was computed as the ratio between MDS and MDD (Li et al., 2017). As in the case of the computation of MDD, MDS and MDP, the two different thresholds, SPI $\le -\mathrm{1}$ and SPI $\le -\mathrm{2}$, were taken into consideration. The effects of the accumulation scale and the spatial patterns were investigated.

Figure 2 Drought characteristic identification using the “run theory” (Yevjevich, 1967).

Figure 3 SPI_6, SPI_12 and SPI_24 for cell no. 2 (southern area – a, c, e) and cell no. 108 (northern area – b, d, f).

3 Results and discussion

3.1 Temporal analysis

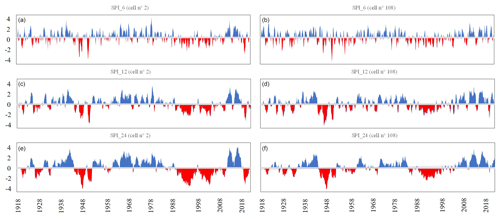
The temporal patterns of the SPI time series in the region under investigation at different timescales have the potential to provide insights into the temporal variation of droughts in the Campania region. As an example, Fig. 3 illustrates SPI_6, SPI_12 and SPI_24 for two cells of the grid data (Fig. 1). In the left panels an example from the southern coastal area is depicted, whereas in the right panels the example is from the northern inland area.

In both areas, Fig. 3 clearly highlights the drought periods that affected the Campania region around 1940–1950 and around 1990–2010. This result appears consistent with a European-scale assessment study in which it was reported that the period between 1985 and 1995 was characterized by the broadest spread of extreme drought events, mainly localized on the Iberian Peninsula, southern Europe, the Balkans and western Turkey (Bonaccorso et al., 2013). Drought severity appears less pronounced in the northern inland areas, especially if looking at the longest accumulation timescale. Drought tends to be more persistent in the southern areas than in northern ones which additionally have been only impacted a little by the drought conditions starting in 2015 in the region. More details about the spatial variability of drought features will be discussed in the following.

Figure 4 SPI MMK test sign for the different accumulation scales (α= 5 %).

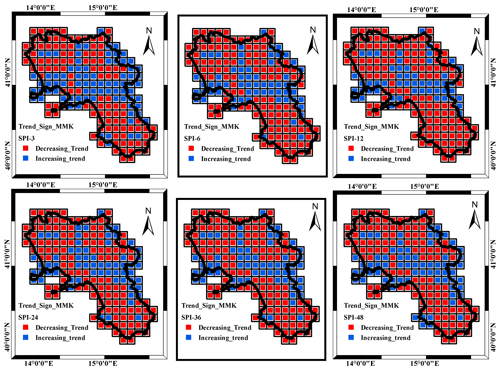
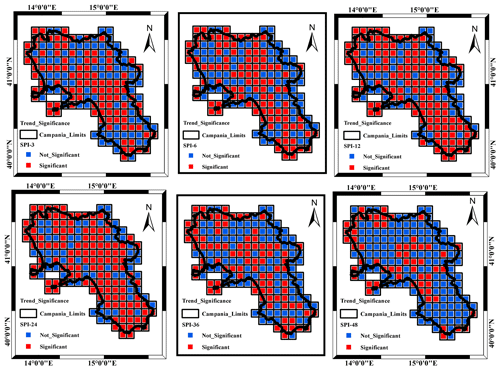
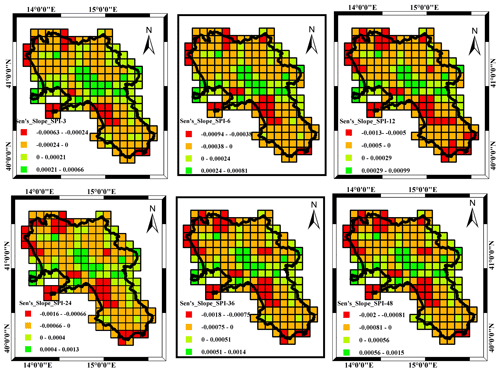
The modified Mann–Kendall (MMK) test and the Sen's slope estimator were carried out to investigate temporal trends, sign, significance and magnitude in SPI time series over the studied period. The relevant results of the MMK for trend sign and significance (significance level = 5 %) are shown respectively in Figs. 4 and 5.

Figure 5 SPI MMK test significance (α= 5 %) for the different accumulation scales.

Starting from the SPI_3 to SPI_12, the downward trend become dominant in the study area and is especially marked in the northwestern and southern sectors of the region (Fig. 4), which correspond to the area featured by the largest mean annual precipitation and the largest precipitation downward trend (Longobardi and Villani, 2010). The proportion of negative to positive trends, with negative values still dominant in over 60 % of the cells, remains almost similar for the SPI_24 to SPI_48.

Concerning the significance of the trend (Fig. 5), the MMK test illustrated how a very large proportion of the gridded SPI showed a significant trend over the different timescales especially from the SPI_3 to the SPI_24 accumulation scale (Fig. 5). For the SPI_3, SPI_6 and SPI_12, the negative trend is particularly significant, with a percentage of grid cells of about 55 % for both SPI_3 and SPI_6 and 65 % for SPI_12. Regarding the spatial distribution of the trend, the SPI_24 is the most significant with almost 70 % of the grid cells. Beyond this scale, temporal variations did not appear significant. As the groundwater systems of the region are characterized by long delay times and thus being potentially impacted by SPI accumulated over a large scale, it is likely that those systems are not strongly impacted by climate temporal variations (Longobardi and Van Loon, 2018). On the national scale, the obtained results were well in line with the general overview outlined in previous research by Delitala et al. (2000) and Bordi et al. (2001) for other regions of southern Italy (Sardinia, Sicily and Puglia) and, furthermore, were in perfect accord with the outcomes given by Buttafuoco and Caloiero (2014) for the Calabria region in southern Italy.

Figure 6 SPI Sen's slope for the different accumulation timescales.

At the regional scale, the results for the modified Mann–Kendall trend test are also consistent with the findings of previous climatological studies concerning precipitation regime investigation (Longobardi and Villani, 2010; Longobardi et al., 2016). In fact, annual and seasonal precipitation in the region were found to be featured by a generalized negative trend during the last century, even though the downward tendencies, contrary to the SPI tendencies, were significant for a very moderate number of rain gauge stations.

The magnitude of the trend in the SPI time series, as assessed using Sen's estimator, is presented in Fig 6. In agreement with the results of the MMK test, the trend was dominantly negative across the region, which is consistent with the trend sign represented in Fig. 4 with some exceptions for a west–east transect at the middle latitudes of the region that correspond to an area which features moderate mean annual precipitation values and the lowest downward precipitation trends (Longobardi and Villani, 2010). On average, the tendency toward drier conditions was however rather moderate and characterized by an amplification with increasing accumulation timescale. The increase in the SPI index amounts to about 10 % in 10 years for the case of SPI_6. It increases up to 15 % and 24 % in 10 years respectively for the case of SPI_12 and SPI_48. The variability in the minimum and maximum assessed trend, on the spatial scale, also increases for increasing accumulation timescale.

3.2 Drought characteristics assessment

Figure 7 shows the total number of drought events detected within the SPI time series from 1918 to 2019 for moderate drought conditions (threshold SPI $\le -\mathrm{1}$) and for extremely severe drought conditions (threshold SPI $\le -\mathrm{2}$) for each point of the grid for all the accumulation scales considered. In the case of moderate drought events, it was observed that the SPI_3 is associated with the largest number of droughts, which was on average 95, for the whole period of observation over the 191 grid cells. Provided the large theoretical autocorrelation in SPI time series for the larger accumulation scale, drought frequency decreased with increasing accumulation scale, with the SPI_24 to SPI_48 patterns almost similar among them (Fig. 7 upper panel). The results appeared in good agreement with those demonstrated by other authors (McKee et al., 1993; Buttafuoco et al., 2015; Marini et al., 2019; Fung et al., 2020). A very similar behavior was found in the case of extremely severe drought episodes except for the lower number compared to the case of moderate events. The average number of drought events in the case of SPI_3 for the threshold SPI $\le -\mathrm{2}$ was on average 27 for the whole period of observation over the 191 grid cells. Concerning the spatial patterns, although a moderate correlation appeared for small cluster of cells, an evident concentration of drought event occurrence in a specific area was not found.

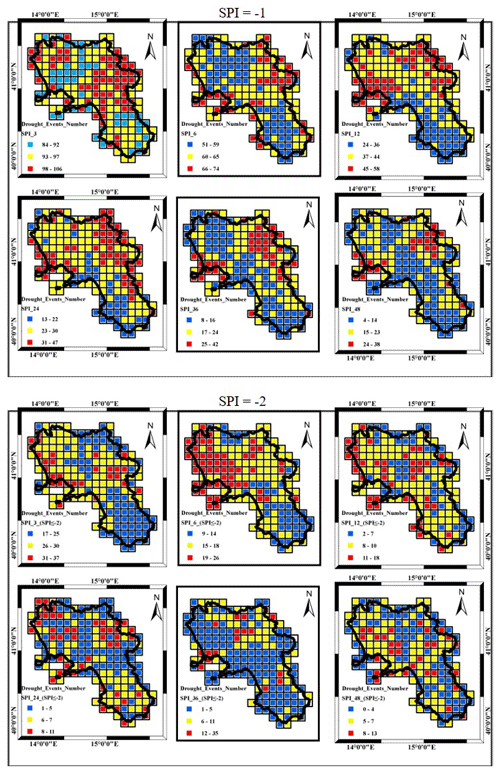
Figure 7 Number of drought events for the different accumulation timescales over the whole period of observation 1918–2019. Upper panels: moderate drought events (SPI $\le -\mathrm{1}$). Lower panels: extremely severe drought events (SPI $\le -\mathrm{2}$).

Figure 8 MDD (mean drought duration) for the different accumulation periods considered (SPI $\le -\mathrm{1}$).

Figure 9 MDS (mean drought severity) for the different accumulation periods considered (SPI $\le -\mathrm{1}$).

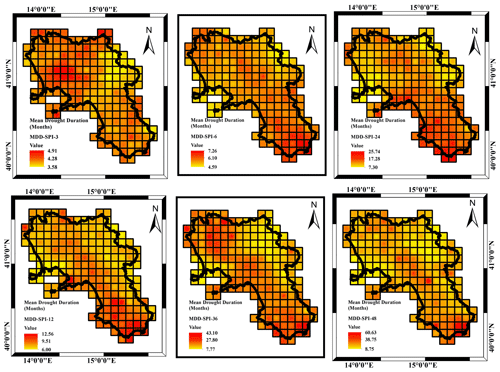
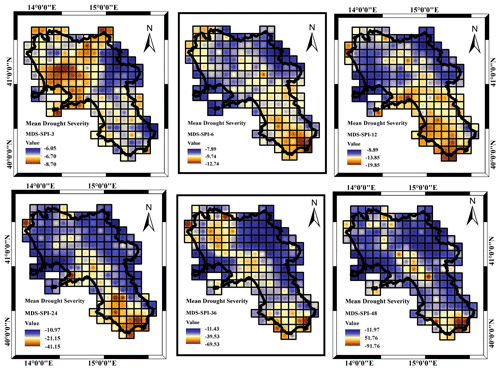
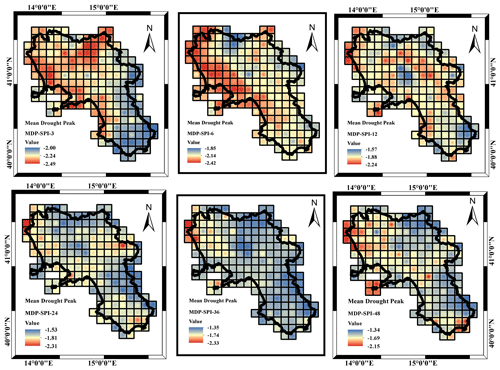
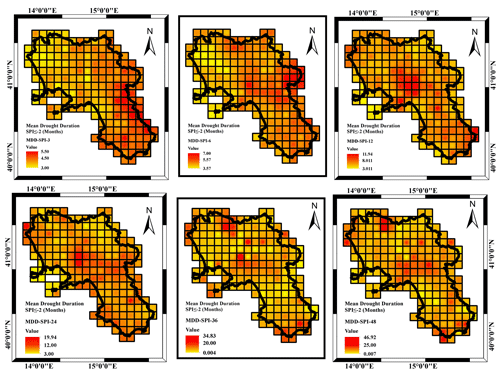
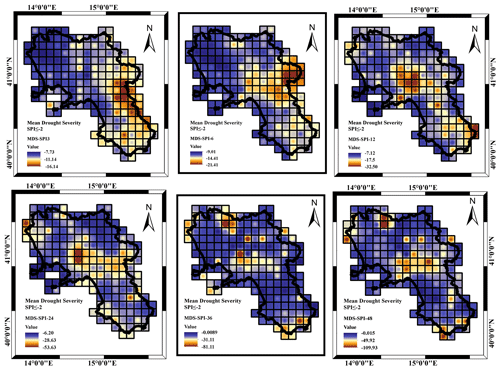
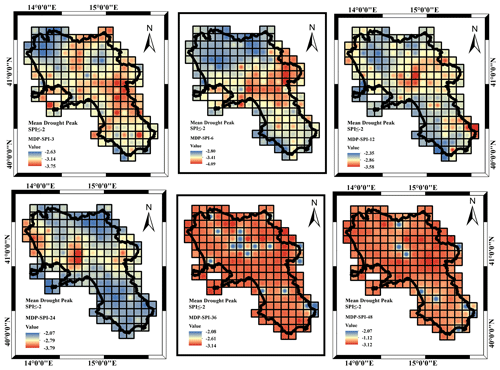
More insights came from the analysis of the MDD, MDS and MDP respectively illustrated in Figs. 8, 9 and 10 with reference to a threshold value of SPI $\le -\mathrm{1}$.

Concerning the MDD (Fig. 8), different from what occurred in terms of drought frequency, the mean drought duration increased with the accumulation timescale, ranging from 4 to 5 months for the SPI_3 to 8 to 60 months for the SPI_48. The accumulation timescale also affected the MDD spatial behavior (Fig. 8). In the case of SPI_3 and SPI_6, almost the whole region was affected by the average MDD values. In the case of SPI_12, SPI_24, SPI_36 and SPI_48, the largest MDD values were detected along a northwest to southeast transect and more evidently in the southern sectors of the region. At the smallest timescales (SPI_3) the northern sections are the most impacted. For the longer accumulation timescales, the maximum values detected in the southern region were mainly caused by severe drought periods which occurred in 1990, 2003 and 2017 in the region.

Figure 10 MDP (mean drought peak) for the different accumulation periods considered (SPI $\le -\mathrm{1}$).

Concerning the MDS (Fig. 9), because of the MDD characteristics, the drought severity increased with the accumulation timescale ranging from 6 to 8 for the SPI_3 to 11 to 90 for the SPI_48 (Fig. 9). The spatial pattern of MDS was affected by the accumulation timescale, such as in the case of the MDD. For the SPI_3, MDS showed a major severity in the northern area, whereas moving from SPI_12 to SPI_48, MDS severity moved from northern to southern areas and almost disappeared with an even distribution set at an almost constant value (about −10).

Concerning the MDP (Fig. 10), because of what was previously observed in the case of the MDD and MDS, the minimum (about −1.5 on average) and maximum (about −2.3 on average) values appeared similar for the different accumulation timescales and were likely more pronounced for the lower accumulation scales where MDP's largest peaks are focused on the northern area. In contrast, the spatial pattern was found to be particularly complex and did not show a clear tendency related to the accumulation timescale (Fig. 10). Overall, the largest peaks are detected in the northern areas of the region for the SPI_3 to SPI_6. From SPI_24 to SPI_48 there was a general tendency for a dominant low peak spatial distribution, with an exception for some coastline areas in the north of the region. The SPI_12 represented a neutral condition, where minimum and maximum SPI values are rather pronounced and spread over the region.

Figure 11 MDD (mean drought duration) for the different accumulation periods considered (SPI $\le -\mathrm{2}$).

Figure 12 MDS (mean drought severity) for the different accumulation periods considered (SPI $\le -\mathrm{2}$).

Figure 13 MDP (mean drought peak) for the different accumulation periods considered (SPI $\le -\mathrm{2}$).

By increasing the threshold for the SPI values, moving from SPI $\le -\mathrm{1}$ to SPI $\le -\mathrm{2}$, it was possible to explore the extremely severe drought conditions over the region.

Concerning the MDD (Fig. 11), the mean drought duration increased with the accumulation timescale, ranging from 3 months for the SPI_3 to 47 months for the SPI_48. Compared to the case of moderate drought events, in the case of extremely severe events the mean drought duration decreased for each accumulation scale. Concerning the spatial distribution, the same consideration provided for the case of SPI threshold $\le -\mathrm{1}$ hold also in the case of SPI threshold $\le -\mathrm{2}$.

With reference to the MDS and consequently to the MDD, the drought severity increased with the accumulation timescale ranging from 16 for the SPI_3 to 109 for the SPI_48 (Fig. 12). Compared to the case of moderate drought events, in the case of extremely severe events the mean drought severity increased for each accumulation scale. Concerning the spatial pattern of MDS, it appeared as a common feature according to which the largest MDS values appeared in the central area of the region, with some spot cells located in the extremely southern and extremely northern coastlines. An exception was provided by the lower SPI_3.

In the end, concerning the MDP (Fig. 13), different to what occurred in the case of the MDD and MDS, the minimum (about −2.5 on average) and maximum (about −3.5 on average) values appeared similar for the different accumulation timescales and likely more pronounced for the lower accumulation scales (−4.09 for SPI_6). The spatial pattern was found to be particularly complex and did not show a clear tendency related to the accumulation timescale (Fig. 13). Larger peaks were still focused in the central area of the region, but the area covered changed with accumulation timescale, being rather moderate for the larger SPI accumulation scale. A large peak appeared to spread all over the region in the case of the largest accumulation periods, SPI_36 and SPI_48.

4 Conclusions

Drought is a sustained period of below-normal water availability. It is a recurring and worldwide phenomenon, but the Mediterranean Basin is seen as a very vulnerable environment in this perspective. The main objective of this study was to assess the drought features in the Campania region of southern Italy through an analysis of the spatial and temporal pattern characteristics of SPI time series, computed at different accumulation scales over a centennial period from 1918 to 2019. The modified Mann–Kendall test and the Sen's test were applied to describe the temporal trend significance and magnitude. Additionally, for both moderate (SPI $\le -\mathrm{1}$) and extremely severe (SPI $\le -\mathrm{2}$) drought conditions, the “run theory” (Yevjevich, 1967) was applied to illustrate drought events frequency, duration, peak and severity.

Concerning the drought temporal features, the trend was found to be dominantly negative, and the percentage of impacted cells increased with accumulation scale. It remained almost similar for SPI time series computed over 24 months or longer intervals. The significance was also found to be particularly evident approaching 70 % of grid cells for SPI_24. Beyond this timescale threshold, significance in temporal variability strongly decreased. The SPI increase over time, ranging from about 10 % in 10 years for the case of SPI_6 and 24 % for the SPI_48. In the case of moderate dry conditions, MDD increased with the accumulation timescale, ranging from about 5 months for the SPI_6 to 60 months for the SPI_48. Accordingly, MDS increased with accumulation scale, moving from about −10 in the case of SPI_6 to about −50 in the case of SPI_48. MDP did not change significantly with the accumulation scale and was particularly pronounced in the case of the shorter temporal scales. Extremely severe events were featured by shorter durations and larger severity compared to the moderate drought events but were much less frequent (over 75 % less then).

Concerning the spatial pattern, the negative trends appeared to occur along a northwest to southeast transect, whereas positive trends were focused along a west–east transect at the middle latitude of the region. These areas are respectively featured by large mean annual precipitation coupled with the largest negative trends and by low to moderate mean annual precipitation and lowest negative trends. Those two regions are quite different in terms of orography. While the first is characterized by mountainous relief approaching or close to the coastline, the second features a large plain devoted to agricultural practices, crossed by the longest river of the region, the Volturno River, which probably represents an access corridor to atmospheric weather systems. The complex orography of the region appears then to impact both the average precipitation spatial distribution and the relevant temporal variability. The accumulation timescale affected the MDD spatial behavior. At the lowest accumulation scale, the northern area appeared to be more affected, whereas large MDD values were detected along a northwest to southeast transect and were however more evident in the southern sectors of the region. The maximum values detected in the southern area for the longer accumulation timescale were mainly caused by severe drought periods occurring in 1990, 2003 and 2017 in the region. The MDS spatial pattern was also affected by accumulation scale. It showed a concentration on the northern region area for the shorter temporal scales and instead a constant spatial distribution for the longer temporal scales, with an exception for a northwest to southeast transect and for the southern sectors of the region where the largest MDS values were detected. In the end, the MDP spatial pattern was found to be particularly complex and did not show a clear tendency related to the accumulation timescale. At least for the shorter timescale, the largest drought peaks seemed concentrated on the norther inland area of the region, which overall could be addressed as an area potentially prone to agricultural drought stress.

The current research illustrated how historical in situ long-term measurements are crucial for understanding historical drought conditions to plan mitigation strategies to further face future climate change impacts.