Predictive skill for atmospheric rivers in the western Iberian Peninsula

A large fraction of extreme precipitation and flood events across western Europe are triggered by atmospheric rivers (ARs). The association between ARs and extreme precipitation days over the Iberian Peninsula has been well documented for western river basins.

Since ARs are often associated with high impact weather, it is important to study their medium-range predictability. Here we perform such an assessment using the ECMWF ensemble forecasts up to 15 d for events where ARs made landfall in the western Iberian Peninsula during the winters spanning between 2012–2013 and 2015–2016. Vertically integrated horizontal water vapor transport (IVT) and precipitation from the 51 ensemble members of the ECMWF Integrated Forecasting System (IFS) ensemble (ENS) were processed over a domain including western Europe and the contiguous North Atlantic Ocean.

Metrics concerning AR location, intensity, and orientation were computed, in order to compare the predictive skill (for different prediction lead times) of IVT and precipitation. We considered several regional boxes over western Iberia, where the presence of ARs is detected in analysis/forecasts, enabling the construction of contingency tables and probabilistic evaluation for further objective verification of forecast accuracy. Our results indicate that the ensemble forecasts have skill in detecting upcoming AR events, which can be particularly useful to better predict potential hydrometeorological extremes. We also characterized how the ENS dispersion and confidence curves change with increasing forecast lead times for each sub-domain. The probabilistic evaluation, using receiver operating characteristic (ROC) analysis, shows that for short lead times precipitation forecasts are more accurate than IVT forecasts, while for longer lead times this reverses (∼10 d). Furthermore, we show that this reversal occurs for shorter lead times in areas where the AR contribution is more relevant for winter precipitation totals (e.g., northwestern Iberia).

1 Introduction

Extreme precipitation events in the Iberian Peninsula are often due to anomalous vertically integrated water vapor transport (IVT) which are generally associated with an atmospheric river (AR; Ramos et al., 2015, 2018; Eiras-Barca et al., 2016). According to the definition of the American Meteorological Society glossary of Meteorology, ARs correspond to “a long, narrow, and transient corridor of strong horizontal water vapor transport that is typically associated with a low-level jet stream ahead of the cold front of an extratropical cyclone. The water vapor in ARs is supplied by tropical and/or extratropical moisture sources and these systems frequently lead to heavy precipitation where they are forced upward – for example, by mountains or by ascent in the warm conveyor belt. Horizontal water vapor transport in the mid-latitudes occurs primarily in atmospheric rivers and is focused in the lower troposphere” (Ralph et al., 2018).

Extreme precipitation and floods in other regions of the world have been shown to be also associated with ARs, especially on the western continental coastlines of the mid-latitudes (Guan and Waliser, 2015; Gimeno et al., 2016). Common regions where ARs strike are the western coast of continents, such as in California (e.g., Gershunov et al., 2017; Ralph et al., 2017; Rutz et al., 2019), South Africa (e.g., Blamey et al., 2018; Ramos et al., 2019), Chile (e.g., Viale et al., 2018, Valenzuela and Garreaud, 2019), the Iberian Peninsula (Ramos et al., 2015; Eiras-Barca et al., 2016), and even southern Australia and New Zealand (Guan and Waliser, 2015; Kingston et al., 2016). However, their climate and socioeconomic impacts are significant also in other regions of the world, such as western and northwestern Europe (Lavers and Villarini, 2013, 2015; Sodemman and Stohl, 2013) and even the east coast of the USA (Mahoney et al., 2016; Miller et al., 2019).

AR impacts are not always hazardous, as they can also be responsible for providing beneficial water supply (e.g., Dettinger, 2013). Lavers and Villarini (2015) show that for western Europe, the west coast of the USA, and for the central and northeastern USA, the AR contribution to total precipitation occurring during the winter months is in the range between 30 % and 50 %. In addition, Ralph et al. (2019), introduced a new scale for the intensity and impacts of ARs along the west coast of the USA, where the authors showed that weak ARs are mostly beneficial, since they can enhance water supply and snowpack, while stronger ARs tend to be frequently hazardous.

Due to its importance to the hydrological cycle, in recent years, there has been an increase in the number of studies dealing with the predictive skill of the different forecast systems in terms of ARs at short- and medium-range forecasts, as well as seasonal to sub-seasonal scales. Regarding short- (1–3 d) and medium-range (3–14 d) forecasts, most studies are focused on the USA. Among them, Nayak et al. (2016) analyzed the skill of global numerical weather prediction models to forecast atmospheric rivers over the central United States showing that, for five different numerical models, AR occurrences are predicted quite well for short lead times, with an increase in the location errors as the lead time increases to about 7 d. The authors show that, as expected, the skill of the forecast decreases with increasing lead time in both occurrence and location.

On the other hand, Martin et al. (2018), examined in detail the skill of a mesoscale numerical weather prediction system (WRF) and compared it with a global numerical weather prediction model (Global Ensemble Reforecast Dataset, Hamill et al., 2013) during AR events for the western USA. It was shown that both models present similar and important errors in low-level water vapor flux, and consequently on the magnitude of precipitation. However, it was found that WRF (at 9 km horizontal resolution) can add value to the forecast when compared with a global numerical weather prediction model by means of dynamical downscaling of the medium-range forecast.

Using an adjoint model framework (Errico, 1997), it was shown for short-range forecast that both low-level winds and precipitation, for ARs striking California, are most sensitive to mid-to-lower-tropospheric perturbations in the initial state in and near the ARs (Doyle et al., 2014; Reynolds et al., 2019). These kinds of studies can help identify locations of greatest sensitivity in the forecast, thus helping to plan observational campaigns that probe ARs using research aircraft and dropsondes; the dropsonde observations will then be assimilated into operational forecast models (Lavers et al., 2018b; Guan et al., 2018).

Weather forecasting uses a process called ensemble forecasting to generate multiple realizations of possible future atmospheric conditions or states. This is undertaken to take into account uncertainties in the initial atmospheric state and inadequacies in the numerical model formulations. In recent years a new approach based on the IVT forecasts (Lavers et al., 2014) has revealed that the IVT may provide earlier awareness of ARs and extreme precipitation than precipitation forecasts in different regions of the world (Lavers et al., 2016, 2017, 2018a). The rationale behind it is using higher IVT predictive skill (e.g., Lavers et al., 2014, 2016) and then using the ECMWF Extreme Forecast Index (EFI, Zsoter et al., 2014). The EFI assesses how extreme the ensemble forecasts are with respect to the model climate and provides values that range between −1 and 1. Regarding the Iberian Peninsula, Lavers et al. (2018a) showed, using a high-density daily surface precipitation observation for the winters of 2015–2016 and 2016–2017, that the IVT EFI has slightly more skill than the precipitation EFI in discriminating extreme precipitation anomalies across the western Iberian Peninsula (Portugal and northwestern Spain) from forecast day 11 onwards. The EFI for IVT became operational at ECMWF in the summer of 2019.

Since the ARs are relatively narrow corridors of strong horizontal water vapor transport, its landfall position will influence the location of a possible extreme precipitation event. In the case of the Iberian Peninsula, it was shown by Ramos et al. (2015) that the occurrence (or not) of extreme precipitation days over western river basins is highly sensitive to the latitudinal location of the AR landfall. Therefore, it is important to obtain an objective assessment of the forecast accuracy at different lead times regarding AR landfall position by using the IVT. This will be explored here through a validation procedure that is based on observational precipitation records.

The main objective here is twofold: (a) to compare the predictive skill of precipitation and IVT at different lead times during extreme ARs striking western Iberia, using ECMWF ensemble forecasts up to 15 d for the winters between 2012–2013 and 2015–2016; and (b) to assess the skill (or accuracy) of IVT probabilistic forecasts in terms of location landfall and intensity, through a probabilistic verification procedure, thus allowing the identification of possible model biases during extreme AR events, and to define simple metrics which may be suitable for operational purposes.

2 Dataset

2.1 Forecast dataset

The ECMWF integrated forecasting system (IFS) ensemble (ENS) operational forecasts were processed for the extended winter seasons (October to March) for four winters: 2012–2013, 2013–2014, 2014–2015, and 2015–2016. ENS has a control run and 50 ensemble members. The two daily forecasts initialized at 00:00 and 12:00 UTC with a lead time of 15 d were processed. The control forecast is produced with the best estimate of the initial atmospheric state. The remaining 50 members are generated by perturbating the initial conditions. The data considered here consist of instantaneous IVT values (for both direction and magnitude), at 00:00 and 12:00 UTC, and 12 h accumulated precipitation centered around these time steps. The IVT was computed using the specific humidity and zonal and meridional winds between the 300hPa and 1000 hPa levels (e.g., Ramos et al., 2015). The ECMWF operational forecasts in the four winters had several upgrades, including model and resolution updates (https://www.ecmwf.int/en/forecasts/documentation-and-support/changes-ecmwf-model, last access: 18 September 2019). A detailed evaluation of the impact of these model changes on forecast skill would have required a detailed analysis of the past forecasts (hindcasts) of each model version, which is beyond the scope of this study.

2.2 Observed precipitation dataset

In order to evaluate the operational forecasts, we have used the Portuguese national network of automatic weather stations surface provided by the Portuguese Institute of Meteorology (Instituto Português do Mar e da Atmosfera, IPMA). The data include 10 min accumulated precipitation from around 100 automatic weather stations over mainland Portugal, which were chosen based on a combination of tests for completeness and quality. The 10 min precipitation were accumulated into consecutive 12 h periods centered at 00:00 and 12:00 UTC of each day. Therefore, the 12:00 UTC covers the precipitation that occurs between 06:00 and 18:00 UTC for the same day, while 00:00 UTC covers the precipitation registered between 18:00 UTC from the previous day and the 06:00 UTC of the following day.

3 Comparing the predictive skill of precipitation and IVT

Firstly, a receiver operating characteristic (ROC, Wilks, 2006) curve analysis was performed for IVT and precipitation forecasts for mainland Portugal. To begin with, using the observed precipitation dataset presented in Sect. 2.2, the mean precipitation (averaged over all mainland Portuguese stations) was computed. Afterwards, a list of extreme precipitation events associated with ARs was obtained by considering observations where the 12 h-cumulated precipitation averaged over Portugal (using the surface stations) exceeded the 95th percentile, considering (i) only events with spatially averaged precipitation > 0.1 mm; (ii) that an AR was detected simultaneously in the region (IVT > 450 kg m⁻¹ s⁻¹), following the threshold found by Ramos et al. (2015) for ERA-Interim reanalysis.

In addition, for the forecasts of extreme IVT and precipitation, we computed the 95th percentile of the corresponding period of analysis (2012–2016). In the computation of the percentiles we took into account the data for the winters spanning 2011–2012 and 2015–2016 and defined the specific percentiles for each forecast day 1 to 14.

These forecasts are then compared against extreme precipitation observations, considering a “yes” forecast if a sufficient number of ensemble members surpass that given threshold. The minimum fraction of ensemble members presenting a yes forecast varies between 0.1 and 1, so that 0.1 means 10 % of the ensemble members have a yes forecast, while 1 corresponds to the totality of the ensemble members. An ROC curve is then obtained by computing hit rates versus false alarm rates (FARs; Wilks, 2006), and considering these different minimum fraction of ensemble members above the 95th percentile. The area under the ROC curve above 0.5 denotes skillful forecasts in respect to climatology. In Fig. 1, the ROC curves and areas for forecasts at different lead times are presented.

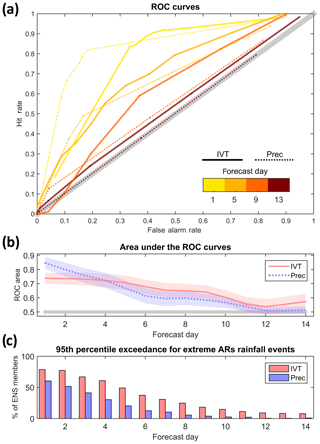
Figure 1 Receiver operating characteristic (ROC) curves for the IVT and precipitation ensemble forecasts during atmospheric river (AR) days from the ECMWF model are shown using Portuguese surface meteorological stations during the extended winters (October–March) of 2012–2016 as a benchmark, and considering events above the 95th percentile (a). The solid lines are for the IVT and dashed lines for precipitation. Different curve colors represent different lead times for the forecasts (1, 5, 9, and 13 d). Area under the ROC curves are shown for lead times up to 14 d (b), where the confidence intervals are also shown. The mean percentage of ensemble members forecasting IVT (pink) and precipitation (purple) above the 95th percentile for lead times up to 14 d during extreme rainfall events associated with ARs (observed precipitation above the 95th percentile associated with an AR over western Iberia) is shown in (c).

The ROC curve analysis (Fig. 1a) clearly shows that lead time is crucial for the performance of both IVT and precipitation forecasts. For both variables, the forecast skill becomes negligible beyond 10 d lead time. While this is not unexpected, our results show that IVT can add potential value to extreme precipitation forecasts during ARs in the medium-range time frame. As shown in Fig. 1b, around day 4–5, ROC areas are higher for IVT than for precipitation, which is also confirmed by the corresponding confidence intervals. These intervals were computed using a bootstrap process (with 1000 repetitions). This result is in line with the work of Lavers et al. (2018a), which highlighted the potential of probabilistic forecasts for IVT (over precipitation forecasts) in western Iberia for two winters over longer lead times. Furthermore, as shown in Fig. 1c, when considering those days with extreme precipitation associated with ARs in Portugal, the number of ensemble members forecasting above the 95th percentile is higher for IVT than for precipitation, for all lead times. Those where the precipitation ROC areas are above the IVT (<5 d) likely reflect a higher number of false alarms using the IVT. In summary, it is clear that between day 5 and 10 the use of probabilistic IVT forecasts can give a significant added value to warnings for extreme precipitation forecasts.

Based on the results presented in Fig. 1, we show that the IVT can provide added value for medium-range operational forecasting of extreme precipitation events. Therefore, from this point onward we will focus our analysis on the performance of the ECMWF probabilistic forecasts for IVT and the AR-related IVT forecasts over Portugal, exploring potential systematic biases, and trying to access model behavior and accuracy metrics at different forecast lead times.

4 Model bias during extreme AR landfall events

We have defined six regional boxes (Fig. 2) over western Iberia, three of them covering the area where IPMA surface stations are located (north Portugal, central Portugal, and south Portugal), and also extending further north and south (sea north, Galicia, and sea south), in order to define metrics for the accuracy of the location of AR landfall, including “hits” and “misses” in forecasts.

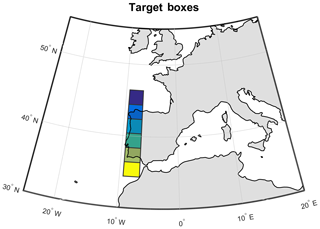
Figure 2 The six regional boxes considered for the verification of IVT probabilistic forecasts in western Iberia at lead times up to 14 d are shown: (i) sea north; (ii) Galicia; (iii) north Portugal; (iv) central Portugal; (v) south Portugal; (vi) sea south.

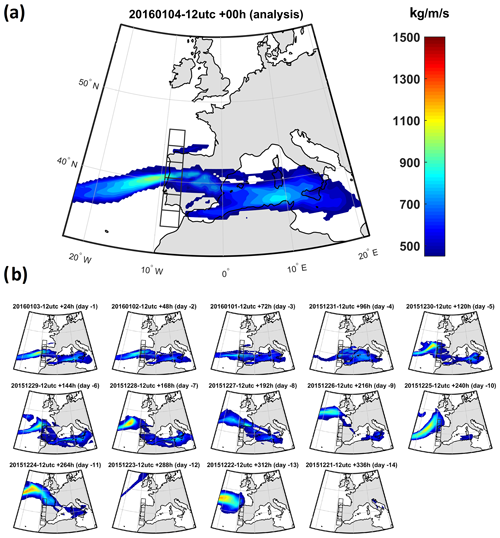
Figure 3 Shown is an example of the evolution of operational forecasting of the IVT in an event affecting western Iberia: (a) analysis of the IVT fields on 4 January 2016 at 12:00 UTC; (b) control forecasts for that date issued with different lead times, from 1 to 14 d.

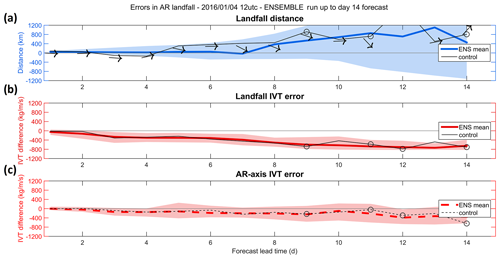
Figure 4 Example of the evolution with lead time for the accuracy of IVT probabilistic forecasts is shown for the event presented in Fig. 3. In (a) the black line represents the error in the location of the maximum IVT (i.e., landfall distance) in the control run (in kilometers), while the solid blue line represents the landfall distance for the ensemble forecasts. The shaded blue envelope shows the ensemble spread, considering the 25th and 75th percentiles. In addition, the black arrows represent the errors in the angle (in degrees) of the AR axis for each forecast. Panel (b) shows the error in the IVT intensity (kg m⁻¹ s⁻¹) for each forecast at the observed landfall location. The solid black line, solid red line, and shaded red envelope are as in (a). Panel (c) shows the error in the maximum IVT at the specific locations where it has been observed and forecasted for each lead time, regardless of the landfall distance. The dashed black line, dashed red line, and shaded red envelop as and (b). The open circles represented in some lead times represent forecasts where the maximum IVT did not surpass a minimum threshold of 450 kg m⁻¹ s⁻¹ within the target domain (i.e., regional boxes over western Iberia).

4.1 Example case study (4 January 2016)

To check the model performance for the IVT forecast over the domain during AR events, we considered only cases where the analysis (zero-hour forecast) exceeded the 450 kg m⁻¹ s⁻¹ threshold for IVT (as defined in Ramos et al., 2015 as where the ERA-Interim dataset was used). These cases were considered as the “benchmark” for model forecast verification, being performed for 00:00 and 12:00 UTC analysis during the four winters spanning 2012–2016. Afterwards, forecasts up to 14 d in advance from the control and ensemble members were compared against the analyses, through the computation of the following metrics that consider the landfall IVT error sensitivity to both intensity and displacement errors:

1. Landfall distance: the meridional distance (in kilometers) between the landfall locations (location of maximum IVT) in the forecast and in the analysis. This value can be positive (negative), indicating a northward (southward) forecast landfall location error.

2. Landfall IVT error: the difference (forecast minus analysis) between the IVT values (in kg m⁻¹ s⁻¹) at the correct location of the landfall, i.e., where the maximum IVT was actually observed in the analysis.

3. AR axis IVT error: the difference (forecast minus analysis) between the IVT values (in kg m⁻¹ s⁻¹) at the specific individual locations of the landfall in the analysis and forecast. It considers the difference in the maximum IVT values in the forecast and the analysis, regardless of where they occur.

4. AR axis angle error: the difference (forecast minus analysis) between the incidence angles (in degrees, respective to west to east) at the specific locations of the landfall (Fig. 2) in the analysis and forecast. The latitude of the maximum IVT is detected for each longitude within the target area. Then, using those latitudes, the “mean” angle is computed, using a west–east direction as the 0^∘ reference. As for other metrics, this is computed for analysis and forecasts, providing the error in the angle. Positive (negative) errors denote a counterclockwise (clockwise) error.

The relevance of these metrics can be easily understood looking at a case study. In Fig. 3a (analysis), an example of an AR affecting the north Portugal box is presented. The 14 small panels (Fig. 3b) show how the control forecast changed with increasing forecast daily lead time. While at short lead times the location, intensity, and angle are quite similar to the analysis, at longer lead times the control forecast becomes less accurate, and some of them predict an IVT magnitude, axis orientation, and landfall totally disconnected from reality. This example highlights the importance of considering ensemble forecasts for long lead times, as discussed below.

The evolution of the forecasts is depicted in Fig. 4, where the metrics for each lead time are summarized using both control and ensemble. As lead time increases, it is notable how the AR was predicted further north by the control forecast (Fig. 4a, black line). In fact, for lead times of 9, 11, and 14 d, there was no predictive skill of an AR affecting the defined boxes (either forecasted much further north, or not forecasted at all, as depicted by the open circles), and in accordance with the corresponding subplot observed in Fig. 3. Consequently, as the landfall distance error increases, the IVT error at that location also increases (black line in Fig. 4b). When considering the AR axis IVT error (Fig. 4c, dashed black line), the decrease with longer lead times is smaller, showing that despite the error in the actual position of the AR, its maximum intensity was well forecasted for most of the period. Regarding the angle of incidence of the AR, it was mostly zonal, both in the analysis and most forecasts, thus with small error. Nevertheless, and as seen in Fig. 3, during medium-range lead times (around 7–10 d) forecasts tended to tilt the AR NW → SE over western Iberia, as depicted by the arrows in Fig. 4a.

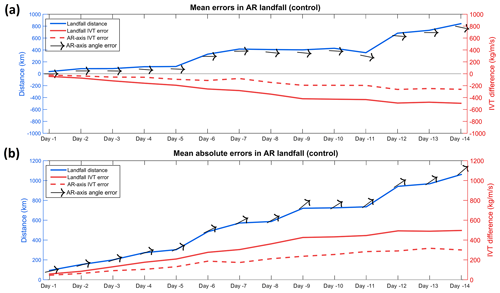
Figure 5 Verification of the accuracy of the control forecast of IVT for all events affecting western Iberia during the extended winters between 2012 and 2016 relative to mean errors (a) and absolute errors (b) is shown. The solid blue line represents the error in the location of the maximum IVT between the observation and each forecast (in kilometers). The solid red line shows the error in the IVT (kg m⁻¹ s⁻¹) for each forecast at the real landfall location (where the maximum IVT was observed), while the dashed red curve represents the error in the maximum IVT between the observed values and each lead time forecast, independent of the location in each forecast. The black arrows represent the errors in the angle (in degrees) of the AR axis.

Moreover, we computed the same metrics described above for each of the 50 ensemble members of ENS; these results are also presented in Fig. 4. The errors of the ensemble mean are presented for landfall distances (solid blue line) and landfall IVT error (solid red line) and AR axis IVT error (dashed black line) as well as the spread in the ensemble forecast (shaded areas), shown here as the 25th and 75th percentiles of the ensemble computed metrics distribution. The control forecast errors and the ensemble mean are in good agreement with the dispersion of the ensemble forecast increasing with lead time. Regarding the landfall distance, it was found that the error increases with lead time, and in this case the control forecast error at a lead time of 12 d is greater than the ensemble mean and even the ensemble dispersion. The 50 members of the ensemble for lead time 5 d (Fig. S1 in the Supplement) and for 12 d (Fig. S2) are shown in Fig. S1 where it can be compared with the control IVT forecast shown in Fig. 3b. One can see that the ensemble members for the shorter lead time are in better agreement and closer to reality. When looking at 12 d lead time (Fig. S2), the dispersion of AR location is much higher when compared with reality and even with the control forecast shown in Fig. 3b. In addition, both landfall IVT error and AR axis error (Fig. 4), for both control and ensemble members, show a decrease in the forecasted IVT as we consider longer lead times.

4.2 Mean performance of the ECMWF forecasts during 2012–2016

In the previous section we analyzed one case study, evaluating both control and ensemble forecasts against analysis. We extended the evaluation of the IVT forecast metrics for all events occurring during the extended winters of the study period (from 2012–2013 to 2015–2016). Similarly to the case study presented in Fig. 4., the same metrics have been computed for all AR landfall cases (207), and the average error is obtained as presented for the control forecast in Fig. 5 and for the ensemble forecast in Fig. 6.

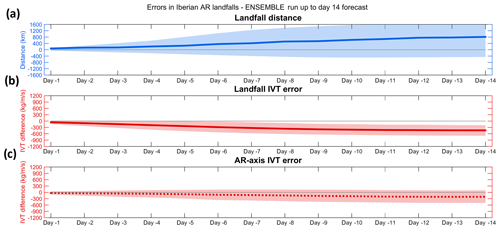
Figure 6 Verification of the accuracy of the ensemble forecast of IVT for all events affecting western Iberia during the extended winters between 2012 and 2016 is shown: (a) mean landfall distance errors (in kilometers) for the mean of the ensemble forecast (solid line) and the spread of the ensemble (shading); (b) as in (a), but for the mean IVT error (in kg m⁻¹ s⁻¹) at the location of observed landfall; (c) as in (b), but at the location of the maximum IVT in each forecast.

When analyzing the control forecast of ARs over western Iberia (Fig. 5), it is possible to identify some systematic errors and biases. Regarding the mean errors (Fig. 5a) a northward landfall bias is systematically found for longer lead times, especially for those longer than 5 d, which can reach up to 800 km at +14 d. In addition, regarding the AR axis angle error, the results show a slightly negative bias in respect to those actually observed. Since we consider the 0^∘ angle as west–east oriented and as AR events over Portugal tend to present a southwest–northeast orientation (Ramos et al., 2015), this systematic bias reflects a lower tilt in the AR orientation at longer time forecasts, or in other words, a tendency for more zonal forecasts (Fig. 5a). When analyzing the IVT magnitude, both landfall IVT error and AR axis IVT error have a negative bias as a result of (i) the error in the landfall location and (ii) an underestimation of the AR intensity. Comparing both metrics in more detail, it can be noted that the AR axis IVT bias is lower than the landfall IVT error, showing that while the IFS forecasts the intensity of the ARs quite well (with just a small underestimation in intensity associated with lead times), the landfall location bias leads to significant IVT forecast errors at the location where the AR actual landfall is observed. The mean absolute errors were also computed for the same metrics (Fig. 5b), unsurprisingly presenting higher errors for landfall distance; location biases occur both northwards and southwards, thus partially canceling themselves, as shown in Fig. 5a. Nevertheless, this difference is not that large, thus reinforcing the systematic tendency for a bias towards the north in longer lead time forecasts. A similar rationale is applicable to the incidence angle, where errors in the tilt of the ARs in different directions tend to cancel out. As such, mean absolute errors tend to be around 45^∘ at longer lead times (Fig. 5b). Overall it is possible to affirm that the case study evaluated in Fig. 4 presents similar biases to those obtain here with the average of the entire set of ARs considered.

The mean weighted errors/biases of the ensemble forecasts (i.e., all the 50 ensemble members) for all events are presented in Fig. 6. The same methodology as in Fig. 4 is followed here, and the ensemble mean is presented, along with the spread in the ensemble forecast (shown here as the 25th and 75th percentiles of the forecast distribution). The results are very similar to the ones found for the control forecast (Fig. 5) with a positive bias (northwards) in the position of the AR landfall as we move to greater lead times, along with a negative bias (less AR intensity) in the landfall IVT error and AR axis IVT error. However, the dispersion in the ensemble forecast is higher in the landfall distance than that in the other IVT error metrics, reinforcing that the model forecasts the ARs but lacks skill in forecasting the right location of their landfall.

It is vital to stress the use of the ensemble forecast in these kinds of conditions. In Figs. 4 and 6, we compare the control forecast with the ensemble mean and the ensemble error metrics. Both control forecast and ensemble forecast landfall and IVT error shows a northerly bias and a negative IVT bias on the landfall location, respectively. Ramos et al. (2016), showed that the number of ARs affecting Iberia is relatively low when compared with the contiguous western France or even the UK using the ERA-Interim reanalysis. This means that on average most of the AR go further north, and the ones hitting Iberia are not that frequent. Taking this into account, one can hypothesize that the northerly bias and respective negative bias in IVT intensity in the AR forecasts at longer lead times can reflect that the model tends to its climatology, which is to have ARs further north, as shown in Ramos et al. (2016). A similar behavior occurs for the blocking frequency (Euro-Atlantic sector and the Pacific sector) using the NCEP Climate Forecast System version 2 (CFSv2), in which for longer lead time the model tends to reach its climatology (Jia et al., 2014).

Figure 7 Shown is the percentage of ensemble members forecasting IVT above 450 kg m⁻¹ s⁻¹ in each of the regional boxes and for each lead time for the case study presented in Fig. 3 (4 January 2016). Green bars represent a spatially accurate forecast (in the box where the maximum IVT was observed). Yellow bars represent a forecast in a box adjacent to where it was actually observed. Red bars represent a forecast in one of the remaining boxes. The bars in the bottom row represent a completely missed forecast, by either (i) no AR forecast or (ii) an AR forecast outside of the six considered boxes in western Iberia.

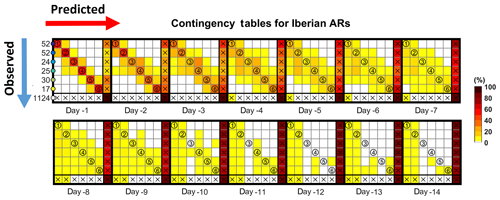
Figure 8 Contingency tables for the accuracy of AR-related IVT forecasts by the ECMWF ensemble system, for lead times ranging between 1 and 14 d, during the winters spanning 2012–2016 are presented. The red shading represents the percentage of observations versus forecasts. Note that a perfect forecast system would only present shadings in the diagonal, as the y axis represents observed events in each box (as presented in Fig. 2) and the x axis represents forecasts in each box. The number of events in each box is shown in the y axis by the blue arrow. The last row and column represent (i) observations/forecasts outside of the six considered boxes and (ii) no AR observed/predicted, respectively.

5 Objective verification of the IVT forecasts

In the previous section we proposed some metrics to analyze control and probabilistic IVT/AR forecast errors in the IFS for the Iberian Peninsula. In this section, we provide an objective verification of the IVT forecast, but considering in greater detail the landfall location and how to use it for a possible application in terms of control forecast for AR landfall. Firstly, and bearing in mind the regional boxes presented in Fig. 2 and the case study presented in Fig. 3, the percentage of ensemble members providing correct/incorrect forecasts regarding the regional boxes is summarized in Fig. 7. As can be seen, the forecast issued the day before the event was almost perfect, with most members predicting the location correctly in the north Portugal box (green bar). As lead time increases, the percentage of correct forecast decreases until day 5, but still a large fraction of members predicts that the AR will make landfall in one of the adjacent boxes (yellow bars), until around day 7. At longer lead times, the percentage of members predicting landfall in boxes further away (red bars) and predicting no landfall or no AR (brown bar) increases significantly.

We now present the contingency table for the ensemble forecasts of IVT for all the events (>450 kg m⁻¹ s⁻¹) during the four winters considered in this study (Fig. 8). Each different box corresponds to a lead time (from 1 to 14 d) and the different boxes correspond to the observed vs. predicted landfall location corresponding the bluish colors correspond to the location of each landfall box shown in Fig. 2. The box for the lead time of 1 d presents additional information to help read the contingency tables: (i) the x axis represents yes forecasts for each box; (ii) the y axis represents yes observations for each box; (iii) the color code presented for lead time of 1 day corresponds to the boxes presented in Fig. 2); (iv) the last column and row, with the white circle and crosses, represent events that have been observed but not predicted and vice versa, respectively. Note that the numbers in the left axis represent the number of observed events in each box. A perfect forecasting model would only present values in the diagonal (N×N).

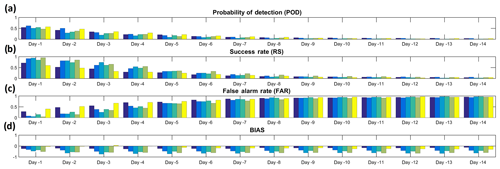
Figure 9 Forecast verification metrics for IVT exceedances (>450 kg m⁻¹ s⁻¹) using the ECMWF ensemble forecast system during the extended winters of 2012–2016 in western Iberia, and for lead times between 1 and 14 d are presented. Colored bars represent metrics for individual regional boxes, where the darkest blue bar represents the northernmost box and the yellow bars the southernmost box (as depicted in Fig. 2).

Results confirm what was partly shown in Fig. 6, as the error in the landfall locations increases with lead time, and an increasing fraction of the ensemble members forecast landfall outside the Iberian Peninsula (further north of Galicia or further south of Algarve) or do not even forecast an AR. However, for shorter lead times (day 1 to day 3) the forecast error is quite low, with the AR landfall being predicted very well, considering the small size of the regional boxes (less than 1^∘ latitude each). In addition, the contingency table also confirms the northward landfall bias of most forecasts, with the left side of the table being more populated, meaning that forecasted location is more frequent in the northern boxes when compared to observations. It is also shown that a few ensemble members pick up the AR; therefore, it can be argued that system IFS is skillful, although with low probability of occurrence in the right location.

Finally, different widely used forecast verification metrics are also computed for the different AR landfall cases, and for each box (as in Fig. 2). The metrics used are the probability of detection (POD), success rate (SR), false alarm rate (FAR), and bias (Wilks, 2006) and their formulation is shown in Fig. S3. As mentioned before, and due to the increase in landfall error with lead time, these systematic errors are also expected to be reflected in the forecast verification metrics. Both POD and RS decrease as lead times increase, getting closer to zero from a lead time greater than 5 d (Fig. 9). Conversely, the FAR is expected to increase with lead time, staying above 0.5 in all boxes from lead times of 5 d or more. The relatively fast decline with lead time in these metrics is not surprising, as they are computed for very small target areas, and this just reflects that a very accurate forecast of landfall location becomes difficult at lead times of greater than 5 d, i.e., when considering the mesoscale. Still, as shown before at a synoptic scale, the model is able to forecast high probabilities of an AR affecting western Iberia at longer lead times. This suggests that an effective warning system can be developed with reasonable lead times, although very detailed local forecasts of AR activity can only be achieved at short timescales.

6 Conclusions

The occurrence (or not) of extreme precipitation days in different river basins is highly sensitive to the latitudinal location of the AR landfall as shown for the Iberian Peninsula (Ramos et al., 2015). This is due to ARs being relatively narrow corridors of strong horizontal water vapor transport; therefore, their landfall position has influence on the occurrence of a possible extreme precipitation event and its specific location. With this in mind, we assessed the forecast accuracy at different lead times regarding AR landfall position, intensity, and incidence angle by using the IVT. To achieve this goal, we used the ECMWF operational ensemble forecasts up to 15 d, for extended winter seasons between the winters of 2012–2013 and 2015–2016, and assessed the skill (or accuracy) of IVT probabilistic forecasts through a probabilistic verification procedure.

The main conclusions are as follows.

• The IVT forecasts show higher predictive skill than precipitation forecasts for lead times greater than 5 d, when considering extreme precipitation events associated with ARs over Portugal. In addition, we show that there is a higher agreement amongst the IVT ensemble members for early awareness at such lead times, than that found for the precipitation ensemble.

• We identified the systematic errors in AR forecasts using an objective verification scheme designed for IVT/ARs applied to the ECMWF ensemble. There is a good predictive skill of the model in terms of AR landfall over the domain for short-term forecasts. However, at longer lead times, the location of the landfall is less reliable, and AR landfall tends to be predicted too far north in the western Iberian Peninsula, and its intensity tends to be underestimated.

• In addition, when using the ensemble members to check the forecast skill for the specific AR landfall locations (using six regional boxes), it becomes clear that the predictive skill at larger spatial scales (the entire domain) tends to be reasonable, while the predictive skill at regional scales tends to be considerably smaller.

• These results show the potential added value to forecast medium-range AR-related precipitation events using the IVT, as well as the possibility to develop warning systems based on IVT ensemble forecasts.

Accordingly, we presented a methodology that can be used in an operational context, consisting of the probabilities of ARs striking different regional boxes. This probability is based on the fraction of ensemble members providing IVT forecasts above a threshold in each box, thus providing an estimate of the probabilities of occurrence and of the expected landfall location. As our analysis for increasing lead times shows, confidence in control forecasts should quickly rise for lead times shorter than a week, but early awareness can be expected at longer lead times. This methodology can be easily replicated using different forecast systems (e.g., the Global Forecast System, GFS) and applied to different regions of the globe after a similar verification as we proposed is performed.