Re-evaluating safety risks of multifunctional dikes with a probabilistic risk framework

It is not uncommon for a flood defence to be combined with other societal uses as a multifunctional flood defence, from housing in urban areas to nature conservation in rural areas. The assessment of the safety of multifunctional flood defences is often done using conservative estimates. This study synthesizes new probabilistic approaches to evaluate the safety of multifunctional flood defences employed in the Netherlands and explores the results of these approaches. In this paper a case representing a typical Dutch river dike combining a flood safety function with a nature and housing function is assessed by its probability of failure for multiple reinforcement strategies considering multiple relevant failure mechanisms. Results show how the conservative estimates of multifunctional flood defences lead to a systematic underestimation of the reliability of these dikes. Furthermore, in a probabilistic assessment uncertainties introduced by multifunctional elements affect the level of safety of the dike proportional to the reliability of the dike itself. Hence, dikes with higher protection levels are more suitable to be combined with potentially harmful uses for safety, whereas dikes with low protection levels can benefit most from uses that contribute to safety.

1 Introduction

1.1 Evolution of the flood risk approach

With rising sea level and an expected rise in extreme rainfall events due to climate change, many regions in the world are faced with increasing flood risk (Bouwer et al., 2010; Hirabayashi et al., 2013). Risk-based approaches towards flood protection have been applied all over the world to inform decision makers on effective flood risk measures in spite of the large uncertainties (Jonkman et al., 2009; Kheradmand et al., 2018; Hall et al., 2003). Nevertheless, a better understanding of the fragility of flood protection measures, including innovative ones like natural flood defences (Temmerman et al., 2013), is instrumental to properly evaluate the flood risk in the future.

The Netherlands in particular is vulnerable to rising flood risks as about 60 % of its area is prone to flooding from the sea or rivers (Kok et al., 2016). After the large flood of 1953 a design water level with an acceptably small exceedance probability was set based on an economic optimization between investment costs and obtained risk reduction (Maris et al., 1961). Many studies have argued for a comprehensive probabilistic approach towards assessing the protection level provided by flood defences (Apel et al., 2006; Vrijling, 2001; Hall et al., 2003). As of January 2017 the water-level exceedance-based national risk standards were replaced by a more complex full probabilistic approach to more effectively adapt to social and economic developments and climate change (Kok et al., 2016). The Dutch Water Act is the first to require the implementation of these principles on a nationwide scale. While these approaches were developed for dikes that serve as flood protection only, in practice many dikes have features serving other functions than flood protection. It is still unclear how such multifunctional aspects of a flood defence must be included in probabilistic safety assessments.

1.2 Multifunctional flood defences

Multifunctional flood defences (MFFDs) are engineered structures designed for the purpose of flood protection while simultaneously enabling other uses (Voorendt, 2017). Combining dikes with other functions is fairly common. Dikes can have roads on top, cables and/or pipelines running through them, or structures on them or are part of a historic landscape. In the Netherlands alone, the majority of dike reinforcement projects already face the presence of more than one function. Usually, enabling multiple functions requires strengthening of the dike beyond the minimal requirements for a traditional dike to account for uncertainties related to those functions (van Loon-Steensma and Vellinga, 2014). Multifunctional use of the flood defence does not need to decrease safety. For example, the development of green foreshores for flood protection services is an attractive option for future climate adaption (van Loon-Steensma et al., 2014) as such flood defences can reduce the risk of flooding through natural processes (van Loon-Steensma and Kok, 2016; van Loon-Steensma et al., 2016).

Flood defences can strengthen other values when functions are properly integrated (Lenders et al., 1999; van Loon-Steensma et al., 2014). In urban areas where space is limited, there is continuous pressure to build on or integrate structures with the flood defence (Stalenberg, 2013). In rural areas, nature-based solutions have gained interest because they combine beneficial properties of natural systems for flood protection (e.g. wave attenuation by vegetation on foreshores) with conservation or development of important natural values (Temmerman et al., 2013; Pontee et al., 2016). In the Netherlands these developments favour the implementation of a multifunctional flood defence due to the limited space and government policy to consider other uses (e.g. natural, historical, and economical) (van Loon-Steensma and Vellinga, 2014).

Despite the large number of multifunctional dikes and incentives, the tools to assess the safety of MFFDs have still been limited to rules of thumb and in-depth tailor-made studies. Unless the multifunctionality is a key feature, assessments are often limited to proving multifunctional use does not significantly diminish the safety of the flood defence, ignoring potential positive contributions to safety. Using such a conservative approach for dike assessments does ensure safe dikes from a flood risk perspective but may result in requiring larger and more expensive dikes.

1.3 Aim

There is a need for improved flood defences due to climate change (rising sea levels, higher river discharges) and socio-economic developments. The number of people exposed to a high risk of flooding is expected to increase from 271 million in 2010 to 345 million in 2050 due to socio-economic growth alone (Jongman and Aerts, 2012). By 2100, 168 million people per year will experience floods due to sea-level rise. By reinforcing dikes this number can already be reduced by a factor of 461 (Hinkel et al., 2013).While reinforcing dike systems, there is plenty of opportunity to enable multifunctional use of the flood defence.

However, the means to determine the safety provided by multifunctional flood defences remain limited to conservative approaches in which multifunctional elements can only be shown to have no significant negative influence. Spurred on by the threat of increasing flood risks by climate change and the revised legislation on flood standards in the Netherlands, a new probabilistic framework to assess multifunctional flood defences is emerging that can be used for a wider context. The aim of this paper is to synthesize the new approaches to evaluate the safety of MFFDs employed in the Netherlands into a single coherent framework and evaluate how this new probabilistic approach towards MFFDs can change the assessed safety compared to the commonly applied conservative approach towards MFFDs .

To this end, first the existing official framework for assessing multifunctional dikes in the Netherlands is analysed and alternative frameworks in both scientific and grey literature for a probabilistic risk-based approach towards assessing MFFDs as required by the new Water Act are explored. These are synthesized in an adapted framework (Sect. 2). Secondly the methods used to calculate the probability of failure of several dikes are explained using the synthesized probabilistic approach and the traditional conservative approach (Sect. 3) to show the differences in assessed safety level (Sect. 4). Finally the implications and results are discussed (Sects. 5 and 6). By illustrating how a probabilistic approach towards multifunctional use can affect the assessed level of safety, new types of integrated solutions can be more fairly compared to monofunctional dikes, both in the Netherlands and beyond.

2 Formulating a framework for MFFD assessment

2.1 Official Dutch guidelines for MFFD dike assessments and design

The methods to assess flood defences in compliance with the official Dutch safety standard are documented in official guidelines (Ministerie van Infrastructuur en Milieu, 2016; Ministerie van Verkeer en Waterstaat, 2007). The assessment can be performed on different levels: basic, detailed, and tailored. Basic assessments are a quick scan with simple rules to approve flood defences with an insignificantly low failure probability. Detailed assessments consist of design formulas and models taken or adapted from Dutch design manuals and are commonly applied for (initial) designs and assessments. These are suitable for predicting the failure of dikes when general descriptions of dike failures can be applied. Such generalizations are not always suitable for MFFDs. Tailored assessments allow for the use of advanced models and experiments outside the guidelines to assess the probability of failure as accurately as possible. These assessments require a large amount of information for a specific location and are generally expensive to perform. The dike needs to pass at least one of these assessments to be considered safe and a proper design ensures the dike will pass the assessments for its entire designed lifespan.

In the official Dutch framework, multifunctional use of the dike is considered either directly as objects on the dike, by the materials used, or indirectly by the geometry of the dike. When only the geometry of the dike is affected or a different material is used (e.g. to integrate with the surrounding landscape) the official framework can still be applied (Slomp et al., 2016). However, if multifunctional use of the dike is facilitated by a non-water retaining object (NWO), e.g. a house or pipeline, an additional assessment must be made for the NWO. For a few multifunctional elements, a basic safety assessment is described in guidelines (structures, vegetation, and traffic) (van Houwelingen, 2012; STOWA, 2000, 2010; TAW, 1994, 1985; Ministerie van Infrastructuur en Milieu, 2016). Only for pipelines is a more detailed assessment available following the Eurocode (NEN, 2012), which ensures the pipeline itself has an acceptably small probability of failure. If a dike cannot be approved by a basic assessment and no suitable detailed assessment is available, a tailored assessment for that specific dike section with NWOs must be made.

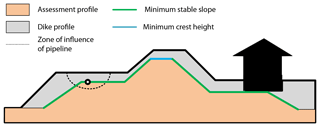
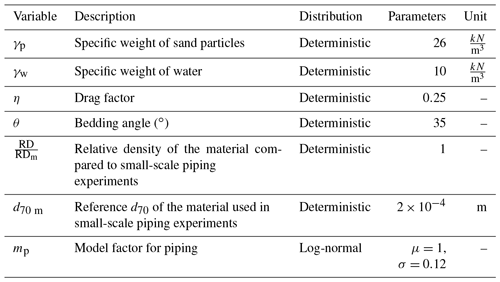
Figure 1 Assessment profile for a dike with NWOs (pipeline and house with basement). Adapted from Fig. A4 of the current Dutch guidelines (Rijkswaterstaat, 2016).

The philosophy of a basic assessment is to rule out the possibility of the NWO affecting the dike significantly. Hence, the dike is considered safe only if the dike is dimensioned such that the zone of influence of the NWO does not extend into the minimum dike profile needed to meet the safety standard (see Fig. 1). As a result, in basic assessments the NWO is always assumed to be in its most critical state during design conditions (e.g. uprooting of a tree). This is the conservative approach to assess the influence of multifunctional elements on safety because the actual probability of multifunctional elements being in a critical state is not considered. The ambition of the Dutch Water Act is to consider the actual probability of flooding which necessitates a risk-based approach to these elements.

2.2 Synthesizing a risk-based approach to MFFD design

The scientific basis for the risk-based framework adopted in the Netherlands was presented by Vrijling (2001). The risk of a flood is decomposed into a fault tree of failure mechanisms, each of which can be described with a mathematical limit state function and evaluated probabilistically. Limit states are common for designing structures in civil engineering and define when a structure collapses resulting in damages and casualties (ultimate limit state) or can no longer perform its intended use (serviceability limit state) (Gulvanessian, 2009). Vrijling's approach of structuring the ultimate limit states of flood defences into a fault tree for risk analyses has been incorporated into many frameworks of flood defences (e.g. Apel et al., 2004; van Gelder et al., 2009; Steenbergen et al., 2004; Vorogushyn et al., 2010) and has already been applied on a large scale to evaluate the Dutch flood defences (Jongejan and Maaskant, 2013). However, the framework was developed for monofunctional flood defences.

Studies on MFFDs specifically are available. However, the developed frameworks address different aspects, like the identification of the degree of spatial and structural integration (Ellen et al., 2011b; Voorendt, 2017; Van Veelen et al., 2015), the identification of costs and benefits (Anvarifar et al., 2013), the identification of the threats and opportunities (Anvarifar et al., 2017), and the identification and evaluation of flexibility for MFFDs (Anvarifar et al., 2016). Other studies on MFFDs tend to only focus on the effects of a specific multifunctional element or failure mechanism (Chen et al., 2017; Bomers et al., 2018; Zanetti et al., 2011). Only recently was an assessment framework specifically for hybrid nature-based flood defences put forward, accounting for multiple failures by putting vegetation-specific equations directly into the assessment procedure (Vuik et al., 2018).

Pending an official framework, practitioners in the Netherlands have used approaches to integrate multifunctional dike elements. One such approach was put forward for trees through the use of scenarios such as uprooting (van Houwelingen, 2012). An approach for assessing NWOs as indirect failure mechanisms with scenarios is being suggested in these cases (Knoeff, 2017). This approach will be explored further in the study.

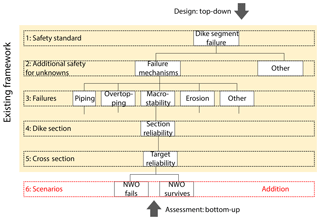
Figure 2 A framework for a detailed assessment and design of a dike with multifunctional elements. The yellow section is the existing framework, while the last step in red denotes the addition of scenarios (e.g. a failed NWO and functioning NWO) to conform to a risk-based approach.

Formulating a practical framework for the assessments of MFFDs is challenging due to the large variety of possible configurations and range of multifunctional elements. Multifunctional elements can be evaluated in different scenarios with simple or complex models in literature while preserving the established structure of the existing Dutch framework. Scenarios in this context are different possible states of a multifunctional element with a probability of occurrence in which the element affects the flood defence. By assessing each scenario and weighing up the probability of failure in each scenario by the probability of the scenario, the probability of failure of the flood defence is calculated accounting for the uncertainty in the state of the multifunctional element. Therefore the steps for MFFD assessments in the Netherlands are synthesized as follows (also see Fig. 2):

• Step 1. Establish the required safety level of the dike segment.

• Step 2. Assign a portion of the required safety level to unknown/unquantifiable risks.

• Step 3. Distribute the remaining failure budget across the known failure mechanisms.

• Step 4. Divide the dike into (close to) homogeneous sections.

• Step 5. Determine a representative cross section and safety level, taking variations along the dike section into account (length effect).

• Step 6 (addition). Determine the scenarios, i.e. states, in which the NWO affects the flood defence differently, assess the probability of these scenarios, and combine them based on their probability of occurrence.

The difference between a basic assessment and a probabilistic one is the addition of Step 6. In a basic assessment, i.e. a detailed assessment without NWOs followed by a basic NWO assessment to exclude significant potential negative influences, first a dike cross section would be designed with the criteria found in Step 1 to 5 and then adapted such that the influence of the intended NWO is outside the designed profile. In the risk-based probabilistic assessment the effects of NWOs are calculated directly with the scenarios in Step 6 and combined with their probability of occurrence to arrive at a safe cross section.

Table 1 The different approaches for assessing the cross section of a multifunctional dike in this study.

3 Application of the risk frameworks

3.1 Comparing the basic assessment with the expanded probabilistic assessment

To answer how a probabilistic approach towards multifunctional dikes can affect the evaluated safety compared to a monofunctional dike, a set of MFFDs is assessed with the new probabilistic approach and the traditional conservative approach (see Table 1 for the approaches). The calculations are performed on a cross-sectional level. The reliability of a cross section is calculated for the most common dike failure mechanisms by probabilistically evaluating the models describing failure for the different scenarios. The failure probabilities per scenario and failure mechanism are combined to arrive at the probability of failure.

Table 2 Overview of failure mechanisms and corresponding methods.

3.2 Failure mechanisms

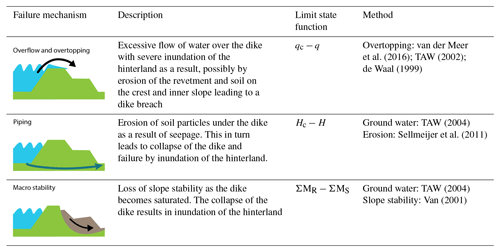
To assess the risk of a flood, it is important to know the mechanisms by which the flood defence could fail. Though many failure mechanisms are possible (Kok et al., 2016), the vast majority of documented dike failures worldwide are the result of three dominant mechanisms: overtopping (resulting in erosion of the inner slope), internal erosion (also referred to as piping), and inner slope stability (Danka and Zhang, 2015; Vorogushyn et al., 2009). Within the Netherlands, predominantly overtopping and slope instability have been the cause of dike breaches in the past (van Baars and van Kempen, 2009). For this study the probability of a flood is calculated by considering the failure mechanisms overtopping, piping, and macro stability (see Table 2). Whether the flood defence fails by a failure mechanism is expressed in an equation called a limit state function:

$$\begin{array}{}\text{(1)}& Z=R-S,\end{array}$$

where Z<0 denotes failure, R is the resistance to failure, and S is the soliciting load.

For overtopping and overflow, the load (S) is the amount of water flowing over the dike, while the resistance (R) is the capacity of the crest and inner slope to resist the flow of water without eroding. For piping, the method of Sellmeijer et al. (2011) is used to calculate the stability of the sand particles in the subsoil under a pore water pressure gradient. It is expressed as a critical head difference (R) that cannot be exceeded by the head difference across the dike (S). Macro stability is calculated within the program D-Geo Stability (Brinkman and Nuttall, 2018) with the stability method by Van (2001) and ground water model by TAW (2004). The method by Van (2001), like the Bishop (1955) method, calculates the sum of the driving moments (S) and the total resisting moment (R) along the slip plane. However, it also accounts for uplift forces on the interface of aquifers present beneath most dikes. The resulting limit states are

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }{Z}_{\mathrm{overflow}\mathrm{\&}\mathrm{overtopping}}=q_{\mathrm{c}}-q\text{(3)}& {\displaystyle }& {\displaystyle }{Z}_{\mathrm{piping}}=H_{\mathrm{c}}-H\text{(4)}& {\displaystyle }& {\displaystyle }{Z}_{\mathrm{macro}\mathrm{stability}}=\mathrm{\Sigma }{\mathrm{M}}_{\mathrm{R}}-\mathrm{\Sigma }{\mathrm{M}}_{\mathrm{S}}.\end{array}$$

Here q_c is the empirically determined critical overtopping discharge, q is the overtopping discharge calculated according the methods of van der Meer et al. (2016) and TAW (2002), H_c is the critical hydraulic head according to Sellmeijer et al. (2011), H is the difference in water level in front and behind the dike, ΣM_S is the sum of the active moments in the critical slip plane, and ΣM_R is the sum of resisting moment in the critical slip plane.

3.3 Probabilistic procedure

Multiple procedures are available for calculating the reliability of a flood defence. A fully probabilistic procedure like Monte Carlo relies on evaluating the limit state function for many variations of the random variables and determines the failure probability as the number of failures over the total number of samples. Meanwhile, a semi-probabilistic approach evaluates the limit state function once and captures uncertainties with (partial) safety factors to determine (non)failure. A probabilistic procedure like the first-order reliability method (FORM) iteratively converges to an approximation of the probability of failure (Hasofer and Lind, 1974). This option was chosen as it does not require millions of evaluations of the limit state function to assess the small failure probabilities required for dikes while still retaining the probabilistic distribution of the variables otherwise lost in a semi-probabilistic approach.

While the FORM procedure can approximate the failure probability of a single limit state function of a single failure mechanism, a combination of failure mechanisms is more complex to evaluate. When the only dependence between failure mechanisms is assumed to be the water level, each failure mechanism becomes an independent event for each discrete water level such that the probability of failure of the system is

$$\begin{array}{}\text{(5)}& {\displaystyle }{P}_{\mathrm{f},\mathrm{sys}\mathrm{|}h}=P_{\mathrm{sys}}\left(f|h\right)=\mathrm{1}-\prod _{i=\mathrm{1}}^n(\mathrm{1}-P_{f,i\mathrm{|}h}),\end{array}$$

where P_f,i|h is the probability of failure given water level h for the ith failure mechanism, and P_f,sys|h is the probability of failure given water level h. Repeating this calculation across all relevant water levels results in the fragility curve of the system to the water level (Bachmann et al., 2013). The failure probability of the system is computed by integrating the fragility curve of the system (F_R(h)) over the probability density function (PDF) of the water level (f_h(h)):

$$\begin{array}{}\text{(6)}& {\displaystyle }{P}_{f,\mathrm{sys}}=\underset{h=-\mathrm{\infty }}{\overset{h=\mathrm{\infty }}{\int }}{f}_h\left(h\right)\times F_{\mathrm{R}}\left(h\right)\mathrm{d}h.\end{array}$$

Equation 6 is discretized to

$$\begin{array}{}\text{(7)}& {\displaystyle }{P}_{f,\mathrm{sys}}=\sum _{j=\mathrm{1}}^{m}P\left(h_j\right)\times P_{\mathrm{sys}}\left(f\mathrm{|}{h}_j\right).\end{array}$$

Low failure probabilities can more easily be expressed in terms of the reliability index which is defined as

$$\begin{array}{}\text{(8)}& {\displaystyle }\mathit{\beta }=-{\mathrm{\Phi }}^{-\mathrm{1}}\left(P_{\mathrm{f}}\right),\end{array}$$

where Φ⁻¹ is the inverse standard normal cumulative distribution function.

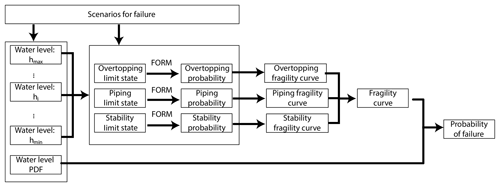
Figure 3 The probabilistic procedure for calculating the probability of failure of a dike cross section in this study.

The probabilistic procedure described above has been utilized before successfully by Lendering et al. (2018) and Bischiniotis et al. (2018) to compute the reliability of canal levees and a cost-optimal river dike respectively. An overview of the entire process as applied in this study is schematized in Fig. 3.

Figure 4 Case studies for comparing the conservative and the new probabilistic approach in this study.

3.4 Case study

3.4.1 Setting and cross sections

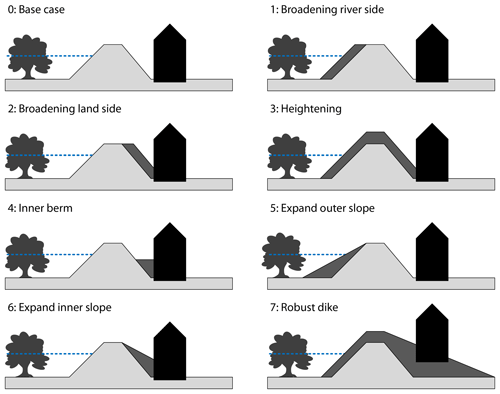
The multifunctional dike for the case study is situated in a riverine area, with nature on the floodplain side and a building on the landward side. To test how a risk approach can affect the calculated level of safety, eight cross sections of multifunctional dike profiles (Fig. 4) are evaluated with three methods: a conservative, a probabilistic, and a monofunctional approach (see Sect. 3.1).

If a dike does not meet the set safety standards, a reinforcement by adapting the profile, among other options, is explored. Each profile in this study represents a common reinforcement strategy. Broadening the dike by widening the crest or expanding the slope reduces the risk of a piping failure by increasing the piping length by a few metres. Furthermore, broadening inwards and making the inner slope shallower makes the inner slope more stable. A berm also improves the stability of the inner slope. Finally heightening the dike decreases the risk of overtopping waves and overflow during high water. The final reinforcement strategy is a combination of heightening and decreasing the steepness of the inner slope.

Each multifunctional element can compromise a section of the dike resulting in failure. For the purpose of this study the multifunctional elements have been simplified so these can be incorporated directly in variables of the limit state functions or dike geometry (see Sect. 3.4.2). When broadening the dike on the floodplain or making a shallow outer slope (see profiles 1 and 5 in Fig. 4), the hinterland remains unaffected by the dike itself, while in the other alternatives, the building becomes part of the flood defence. By reviewing the options the effect of the multifunctional elements on the safety after the reinforcements is evaluated in each framework.

3.4.2 Schematization of multifunctional elements

Effects of multifunctional elements on dike failure are incorporated through scenarios based on the fact sheet by Knoeff (2017). For each mechanism, scenarios are defined in which the element (e.g. tree, structure, and pipeline) affects the failure mechanisms. The probability of failure can then be calculated for each scenario. The total probability of failure for the specific mechanism is computed by weighing the probability of failure of each scenario with the probability of the scenario.

A natural floodplain can add ecological, landscape, and recreational values to the flood protection system. However, elements like trees can penetrate the clay top soil, resulting in cavities within the clay when the tree dies (Zanetti et al., 2011). Following a conservative estimation for the uprooting of trees by TAW (1994), a 2 % annual probability of a cavity within the floodplain is assumed. If a cavity is present, the effective length for piping is reduced to the distance between the dike's inner toe and the location of the disturbance. The trees on the floodplain do not affect the inner slope stability, nor is the tree density in the case study high enough to expect an influence on overtopping by wave dampening properties of trees.

Table 3 Variation in parameters between reinforcement strategies.

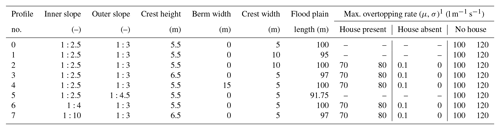
¹ Parameters of the log-normal distribution based on van Hoven (2015).

A building on or close to the dike affects multiple failure mechanisms. The weight of the structure is transferred to the underlying soil, where the load increases friction with the subsoil, increasing slope stability, and lateral stress on the soil, decreasing slope stability. On the slope itself, the structure affects the overtopping mechanism through the inner slope cover that prevents erosion. When a structure is present, it acts as a discontinuity in the outer grass cover such that water can more easily erode soil during overtopping and is reflected in a lower critical overtopping rate. When a structure is absent, the space occupied by it in the profile is assumed to be empty. Furthermore there is no grass cover but instead loose bare soil with practically no overtopping resistance (see Table 3). In the case study the effect of the structure on piping is insignificant as it does not penetrate the aquifer, and pipes can still develop along the outside of the structure rather than directly beneath it.

The structure in the case study is located 3 m behind the inner dike toe. The structure is taken to be 15 m wide, exerts a weight of 17 kN m⁻¹, and is embedded 1 m into the soil on a shallow foundation without additional geotechnical measures like piles or sheet pile walls. The horizontal position of the structure remains fixed for each reinforcement strategy, while vertically the landward end of the structure is always embedded only 1 m in the soil when the dike is expanded inwards. The probability the structure is absent during a high water event is estimated to be 1 %. This probability is based on the percentage of houses demolished in the Netherlands annually which has varied between 0.13 % and 0.23 % per year (van der Flier and Thomsen, 2006) rather than the probability of structural failure of the house. The structure in its demolished state leaves a discontinuity in the dike profile, exerts no weight on the dike, and exposes bare clay on the dike slope while leaving the remaining dike intact.

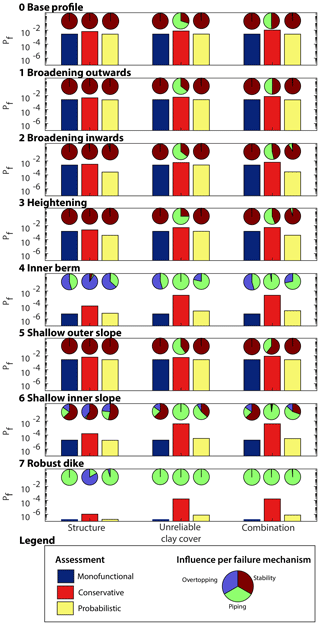
Figure 5 The probability of failure (P_f) for every dike profile (0 to 7) assessed as a monofunctional dike (blue bar), a multifunctional dike with a conservative approach (red bar), and a multifunctional dike using a probabilistic approach (yellow bar) in the situation in which a structure is present (left), an impaired clay cover on the floodplain could be present (middle), and both a structure and unreliable clay cover are present (right). The influence of the three failure mechanisms overtopping (blue), piping (green), and stability (red) is given per bar with a pie chart.

4 Results

The results are presented in Fig. 5. As expected, the conservative approach consistently yields the highest probabilities of failure for the assessed dikes. Both the probabilistic assessment of the additional multifunctional uses and the monofunctional assessment yield a lower probability of failure for each dike profile (Fig. 5).

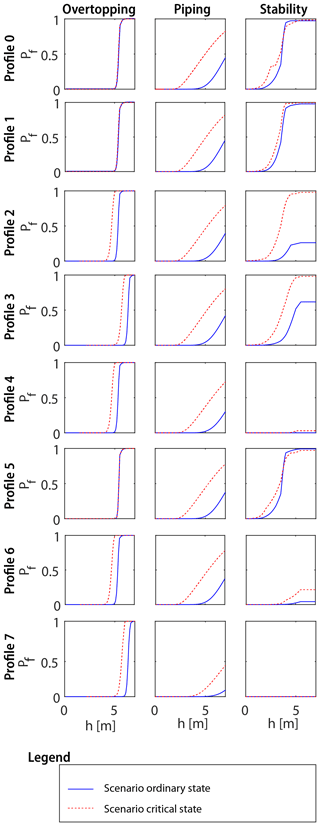
Figure 6 The difference between the fragility curves of the three failure mechanisms and each profile, with both multifunctional elements intact in blue and both multifunctional elements in a critical state in red.

4.1 Slope stability

The weight of the structure can improve the slope stability of the dike in the probabilistic assessment as shown in the assessment of profile 1 with the structure only. The changes in annual failure probabilities are solely due to the presence or absence of weight increasing friction in the passive zone of the slip circle. In the conservative approach the weight of structure is always ignored, leading to a noticeably higher failure probability. This effect is most noticeable in profile 2 with only a structure. The reliability increases by a factor of 10 in the probabilistic assessment compared to a monofunctional dike due to a favourable position of the structure in the critical slip circle (see Fig. 6). In contrast to profile 2, in profile 4 the position of the structure is detrimental to stability, whereby a monofunctional dike has a reliability that is 3 times larger ($\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{8}}$ versus $\mathrm{5.0}\times {\mathrm{10}}^{-\mathrm{8}}$) for the probabilistically assessed dike with a structure. Both the structure and berm add weight, but the structure has the risk of being absent while the risk of a monofunctional berm being absent is negligible. This makes the berm a safer option. Nevertheless this effect on the reliability of profile 4 was insignificant compared to the overall failure probability, which was dominated by piping and overtopping.

4.2 Overtopping

The presence or absence of the structure had a minor impact on overtopping as can be seen in Fig. 6. This is mainly the result of the relatively high predictability of the mechanism itself (reflected by the steepness of the fragility curve) rather than the direct influence of the structure on the mechanism (reflected by the shift of the fragility curve) or additional uncertainty introduced by the structure (reflected by a decreasing steepness of the fragility curve). Because overtopping has a steep fragility curve, the influence of the structure only affects a limited range of water levels, and thus the net effect of the structure on the safety of the dike is limited.

4.3 Piping

Including uncertainty because of unmanaged vegetation on the floodplain has a large effect on piping failure, which was ignored in the assessments with the structure. Because the floodplain in the case study is wide, a scenario with a cavity close to the dike results in a major reduction of the piping length in the probabilistic assessment. Figure 6 shows a large difference between the fragility curves of the critical state and the ordinary state. The presence of trees on the floodplain on piping is even more pronounced in the conservative approach because the entire width of the floodplain is automatically excluded in the assessment. This leads to a different assessment of the need for piping specific reinforcement measures, in particular for the conservative assessment. Due to the dominance of the piping failure mechanism in a conservative schematization, there is an increasing discrepancy between the conservative assessment and the other assessments.

4.4 Assessments

Finally the difference in probability of failure between a monofunctional dike and a multifunctional dike depends on the reliability of the monofunctional dike itself. Unless there are large differences in the schematization of a failure mechanism (as was discussed for piping), differences in failure probabilities between assessments scale roughly by the same order of magnitude as the decrease in failure probability after a reinforcement (Fig. 5; note the log scale for the probability of failure). However, the relative differences become more pronounced leading to proportionally higher failure probabilities in a conservative assessment compared to a probabilistic assessment.

5 Discussion

The results show a large difference between the reliability assessed between the conservative approach and the probabilistic approach. A prevailing view against the multifunctional use of flood defences is that these require larger dimensions to meet the same safety standard as a traditional dike (Ellen et al., 2011a; van Loon-Steensma and Vellinga, 2014). However, as the case study above illustrated, this perception only holds true for a conservative approach that omits multifunctional elements from the assessment. With a more probabilistic approach towards multifunctional elements, their perceived negative influence was significantly smaller or could even result in a net positive influence. Positive contributions of multifunctional elements under likely conditions can be included as well as the likelihood of the multifunctional elements affecting the flood defence negatively.

A drawback of the probabilistic approach is that it needs specific information about the failures and states of multifunctional elements before an assessment can be conducted. For example, erosion around or over discontinuities during overtopping (possibly due to the presence of multifunctional elements like a road) is highly variable and hard to capture in a generic limit state function, even with well-calibrated models (Hoffmans et al., 2009; Bomers et al., 2018). Depending on the sensitivity of the failure probability to these processes, assumptions on effects and statistical distributions would need to be increasingly conservative to guarantee the safety level is met. However, new information on the interaction between multifunctional uses and failure mechanisms is becoming increasingly available through ongoing research (Aguilar-López et al., 2018; Vuik et al., 2018). Furthermore, new techniques are being employed to continuously monitor the dikes in detail (Hanssen and van Leijen, 2008; Herle et al., 2016), while advances in remote sensing allow for closer monitoring of the state of foreshores (Niedermeier et al., 2005; Friess et al., 2012). As a result, a probabilistic approach towards multifunctional elements can capitalize on these advances by updating the previously assumed risks in assessments with observations of the actual performance of MFFDs over time.

Aside from the effects of multifunctional elements themselves, other uncertainties influence how much the multifunctional use of the flood defence can affect the level of safety. For piping, Aguilar-López et al. (2015) demonstrated that by reducing the uncertainty in the seepage properties of the soil of a multifunctional dike, the probability of a piping failure is already significantly reduced. Lanzafame (2017) concluded variability introduced by vegetation only has a small effect on the probability of a slope failure due to larger uncertainties in strength and seepage of the soil. In contrast, a relatively small disturbance by burrowing animals in a fragile dike has resulted in a breach under conditions it had previously survived (Orlandini et al., 2015). The observation that the dike's own reliability influences the degree to which multifunctional use can affect the probability of failure of the dike was also found in this study. As the reliability of the dike itself increases, the influence of a multifunctional element on the level of safety decreases as the added variability of the multifunctional element becomes smaller compared to the uncertainties in other parameters the dike was already designed for. This effect of dike reliability on the influence of multifunctional elements has implications. An increase in failure probability due to multifunctional elements is likely to be overestimated in a traditional assessment for dikes with a high protection level, while similarly for these dikes also only a limited decrease in failure probability can be expected from beneficial multifunctional elements. Conversely, dikes with a low protection level are influenced more by both beneficial and detrimental effects of multifunctional use of the flood defence.

This study only looked at the effects of multifunctional use on flood protection. However, multifunctional use comes with its own set of requirements that must be taken into account. For example, structures need to comply with building codes, and flood protection measures in nature reserves can be subject to environmental protection regulations, while to preserve landscape values substantial dike heightening may be unacceptable. How much such additional non-flood protection requirements influence the design of dikes needs to be researched for a successful implementation of MFFDs.

This study investigated the assessments of multifunctional flood defences for the current situation. In the design of these defences, however, future conditions, like for example climate change or societal trends, need to be taken into account. Scenarios for future sea-level rise in the coming century vary between 0.23 and 0.98 m (IPCC, 2013). Incorporating beneficial multifunctional uses of flood defences, either natural like marshes or man-made like structures, can become an asset to achieve the levels of flood protection needed in the future.

6 Conclusions

This study analysed how a full probabilistic approach towards multifunctional flood defences can change the assessed safety compared to the commonly applied conservative approach in which multifunctional use of the flood defence can only be shown to have no significant negative influence. Although probabilistic assessments have been used before, the new regulations of the Water Act in the Netherlands necessitate a full probabilistic assessment of flood defences. Therefore, a probabilistic framework incorporating multifunctional elements probabilistically was developed. The overall conclusion is that application of a probabilistic approach towards multifunctional use of the flood defence will lead to a lower assessed risk of flooding compared to conservative assessments because (1) positive contributions of multifunctional elements to safety can be included, even when in a critical state there is a negative contribution to safety, and (2) the risk of multifunctional elements being in such a critical state is made explicit. Another important aspect is that effects of multifunctional use on safety become smaller as the reliability of the dike increases. Therefore, monofunctional dikes which already have a high reliability are more suitable to be combined with multifunctional uses detrimental to safety, whereas dikes with a low reliability can benefit more from multifunctional uses that contribute to safety.

Based on the results, we recommend that a probabilistic framework is further developed and implemented for including multifunctional elements into dike assessments. While many knowledge gaps are still present in quantifying the effects of multifunctional use of flood defences, incorporating scenarios in which a multifunctional element can harm or help flood protection can already provide insights in synergies that can be exploited or dangers that can be mitigated. These scenarios and associated probabilities will need to rely on expert judgment. However, it is expected that with the growing number of methods to monitor dike performance and ongoing studies on dike failures, these gaps can be filled in the future. To this end, further research is required on the proper scenarios and their associated probabilities that can be used to improve future assessments of multifunctional dikes. Additionally, more research is needed to assess how multifunctional elements influence the safety of dikes over longer periods, especially in relation to the large uncertainties involved in climate change. A real-world case study for design should be used to explore how these aspects can be incorporated in practice.

Appendix A: Case study parameters

The dike geometry of the base case is captured by the variables in Table A1.

The soil was divided into three layers: the dike core, the blanket layer, and the aquifer. Representative values for the soil layers were taken from known soil types in the Dutch riverine area (Tables A2, A3, and A4).

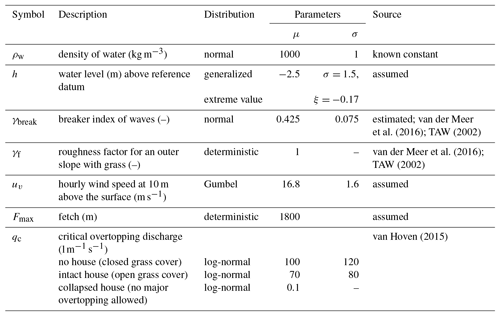
Hydraulic load parameters are given in Table A5. Representative water and wind characteristics were estimated from the hydraulic loads database of the upper Rhine area in the Netherlands, which is available as part of the WBI software. For simplification, the wind direction is only considered in the direction perpendicular to the dike.

Table A1 The standard geometry parameters for the dikes in the hypothetical case study.

Table A2 Standard parameters of the blanket layer for the dikes in the hypothetical case study.

Table A3 Standard parameters of the aquifer layer for the dikes in the hypothetical case study.

Table A4 Standard parameters for the dike soil material for the dikes in the hypothetical case study.

Table A5 Standard hydraulic load and resistance parameters for the dikes in the hypothetical case study.

Appendix B: Overflow and overtopping limit state function

Overflow is calculated directly from the water level (h) and crest height (z_crest) by the formula for a broad crested weir:

$$\begin{array}{}\text{(B1)}& {\displaystyle }{q}_{\mathrm{overflow}}=\sqrt{\mathrm{2}g}\times {\displaystyle \frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}}(h-z_{\mathrm{crest}}{)}^{\frac{\mathrm{3}}{\mathrm{2}}}.\end{array}$$

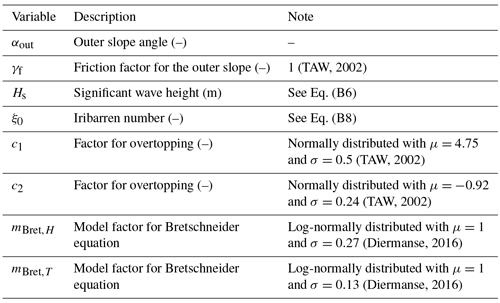
To calculate the overtopping discharge, first the significant wave height (H_s) and period (T_s) perpendicular to the dike are estimated from the water depth (h), fetch length (F), and wind speed (u_wind) with the equations of Bretschneider as presented by Holthuijsen (1980):

$$\begin{array}{ll}\text{(B2)}& {\displaystyle }& {\displaystyle }{F}_x={\displaystyle \frac{gF}{u_{\mathrm{wind}}^{\mathrm{2}}}}\text{(B3)}& {\displaystyle }& {\displaystyle }{h}_x={\displaystyle \frac{gh}{u_{\mathrm{wind}}^{\mathrm{2}}}}\text{(B4)}& {\displaystyle }& {\displaystyle }{p}_{\mathrm{1}}=\tan h\left(\mathrm{0.53}\times h_x^{\mathrm{0.75}}\right)\text{(B5)}& {\displaystyle }& {\displaystyle }{p}_{\mathrm{2}}=\tan h\left(\mathrm{0.833}\times h_x^{\mathrm{0.375}}\right)\text{(B6)}& {\displaystyle }& {\displaystyle }{H}_{\mathrm{s}}=\mathrm{0.283}\times {\displaystyle \frac{u_{\mathrm{wind}}^{\mathrm{2}}}{g}}\times p_{\mathrm{1}}\times \tan h\left(\mathrm{0.0125}\times {\displaystyle \frac{F_x^{\mathrm{0.42}}}{p_{\mathrm{1}}}}\right){\displaystyle }& {\displaystyle }\times m_{\mathrm{Bret},\mathrm{H}}\\ \text{(B7)}& {\displaystyle }& {\displaystyle }{T}_{\mathrm{s}}=\mathrm{7.54}\times {\displaystyle \frac{u_{\mathrm{wind}}}{g}}\times p_{\mathrm{2}}\times \tan h\left(\mathrm{0.077}\times {\displaystyle \frac{F_x^{\mathrm{0.25}}}{p_{\mathrm{2}}}}\right){\displaystyle }& {\displaystyle }\times m_{\mathrm{Bret},\mathrm{T}}.\end{array}$$

Table B1 Description and values of variables in the overtopping and overflow limit state function.

With the wave characteristics, the average overtopping discharge is calculated following the formulas by TAW (2002) and van der Meer et al. (2016). Since no berm is present on the dike of the case study and waves are assumed to be perpendicular, factors related to these aspects are omitted.

$$\begin{array}{ll}\text{(B8)}& {\displaystyle }& {\displaystyle }{\mathit{\xi }}_{\mathrm{0}}={\displaystyle \frac{\tan \left({\mathit{\alpha }}_{\mathrm{out}}\right)}{\sqrt{\frac{\mathrm{2}\mathit{\pi }{H}_{\mathrm{s}}}{g{T}_{\mathrm{s}}^{\mathrm{2}}}}}}\text{(B9)}& {\displaystyle }& {\displaystyle }{q}_{\mathrm{1}}=min{\displaystyle }& {\displaystyle }\left(\begin{array}{c}{\displaystyle \frac{\mathrm{0.067}}{\sqrt{\tan {\mathit{\alpha }}_{\mathrm{out}}}}}\times {\mathit{\xi }}_{\mathrm{0}}\times \exp \left(c_{\mathrm{1}}\times {\displaystyle \frac{z_{\mathrm{crest}}-h}{H_{\mathrm{s}}}}\times {\displaystyle \frac{\mathrm{1}}{{\mathit{\xi }}_{\mathrm{0}}\times {\mathit{\gamma }}_{\mathrm{f}}}}\right)\\ \mathrm{0.2}\times \exp \left(-\mathrm{2.6}\times {\displaystyle \frac{z_{\mathrm{crest}}-h}{H_{\mathrm{s}}}}\times {\displaystyle \frac{\mathrm{1}}{{\mathit{\gamma }}_{\mathrm{f}}}}\right)\end{array}\right)\\ {\displaystyle }& {\displaystyle }\times \sqrt{g\times H_{\mathrm{s}}^{\mathrm{3}}}\\ \text{(B10)}& {\displaystyle }& {\displaystyle }{q}_{\mathrm{2}}={\displaystyle }& {\displaystyle }{\mathrm{10}}^{c_{\mathrm{2}}}\times \exp \left(-{\displaystyle \frac{z_{\mathrm{crest}}-h}{{\mathit{\gamma }}_{\mathrm{f}}}}\times H_{\mathrm{s}}\times \left(\mathrm{0.33}+\mathrm{0.022}\times {\mathit{\xi }}_{\mathrm{0}}\right)\right)\\ {\displaystyle }& {\displaystyle }\times \sqrt{g\times H_{\mathrm{s}}^{\mathrm{3}}}\\ \text{(B11)}& {\displaystyle }& {\displaystyle }{q}_{\mathrm{overtopping}}=\left\{\begin{array}{cl}{q}_{\mathrm{1}}& {\mathit{\xi }}_{\mathrm{0}}<\mathrm{5}\\ {\mathrm{10}}^{\frac{\log \left(q_{\mathrm{1}}\right)+\log \left(q_{\mathrm{2}}\right)}{\mathrm{2}}}& \mathrm{5}\ge {\mathit{\xi }}_{\mathrm{0}}\ge \mathrm{7}\\ q_{\mathrm{2}}& {\mathit{\xi }}_{\mathrm{0}}>\mathrm{7}\end{array}\right.\end{array}$$

A description and values for the variables are presented in Table B1.

The limit state function is then evaluated as

$$\begin{array}{}\text{(B12)}& {\displaystyle }{Z}_{\mathrm{overflow}\mathrm{and}\mathrm{overtopping}}=q_{\mathrm{c}}-q_{\mathrm{overflow}}-q_{\mathrm{overtop}}.\end{array}$$

Appendix C: Piping limit state function

Piping is evaluated with the piping erosion formulae of Sellmeijer et al. (2011). The critical head difference (H_c) is calculated as

$$\begin{array}{}\text{(C1)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{R}}={\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{p}}-{\mathit{\gamma }}_{\mathrm{w}}}{{\mathit{\gamma }}_{\mathrm{w}}}}\times \mathit{\eta }\times \tan \mathit{\theta }\times {\left({\displaystyle \frac{\mathrm{RD}}{{\mathrm{RD}}_{\mathrm{m}}}}\right)}^{\mathrm{0.35}}\text{(C2)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{S}}={\displaystyle \frac{d_{\mathrm{70}}}{\sqrt[\mathrm{3}]{\mathit{\kappa }L}}}\times {\left({\displaystyle \frac{d_{\mathrm{70}\mathrm{m}}}{d_{\mathrm{70}}}}\right)}^{\mathrm{0.6}}\text{(C3)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{G}}=\mathrm{0.91}\times {\left({\displaystyle \frac{d_{\mathrm{aquifer}}}{L}}\right)}^{\frac{\mathrm{0.28}}{{\left(\frac{d_{\mathrm{aquifer}}}{L}\right)}^{\mathrm{2.8}}-\mathrm{1}}+\mathrm{0.04}}\text{(C4)}& {\displaystyle }& {\displaystyle }{H}_{\mathrm{c}}=F_{\mathrm{R}}\times F_{\mathrm{S}}\times F_{\mathrm{G}}\times L.\end{array}$$

Failure occurs when the critical head level (H_c) is exceeded by the head difference (H) and the resistance of the blanket layer:

$$\begin{array}{}\text{(C5)}& {\displaystyle }{Z}_{\mathrm{piping}}=m_{\mathrm{p}}\times H_{\mathrm{c}}-(H-\mathrm{0.3}\times d_{\mathrm{blanket}}).\end{array}$$

The variables introduced by Eqs. (C1) to (C5) are given in Table C1 and are based on estimates used in Dutch dike assessments. The intrinsic permeability (κ) is directly converted from the permeability of the aquifer (k_aquifer).

Table C1 Description and values of variables in the piping limit state function.

Appendix D: Macro stability limit state function

The macro stability of the dike is evaluated using the schematization of the phreatic surface of a clay dike from the TAW (2004) following the official Dutch guidelines (see Fig. D1). The TAW (2004) schematization assumes a drop in the phreatic surface on the interface of the dike with the outside water (1 m as by default) and a linear drop towards the inner toe. The water head in the aquifer was calculated using the equations by TAW (2004) as implemented in the D-Geo Stability software (Brinkman and Nuttall, 2018).

The stability of the slope is calculated with the method by Van (2001) for the slip plane and works on the same principle as the method by Bishop (1955). The main difference between the methods is the separation of the slip plane in an active circle connected by a straight section followed by a passive circle. The centres of these circles of the critical slip plane (R_A and R_P) are found iteratively using the D-Geo Stability software (Brinkman and Nuttall, 2018).

The slip plane is divided into slices, and the net force induced by each slice is calculated. If the moment induced by the active slices (ΣM_S) is greater than the combination of friction forces and moments induced by the passive slices (ΣM_R), the slope is unstable. This is both expressed in a factor of safety (F_S) and a Z function.

$$\begin{array}{}\text{(D1)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{S}}={\displaystyle \frac{\mathrm{\Sigma }{\mathrm{M}}_{\mathrm{R}}}{\mathrm{\Sigma }{\mathrm{M}}_{\mathrm{S}}}}\text{(D2)}& {\displaystyle }& {\displaystyle }{Z}_{\mathrm{macrostability}}=F_{\mathrm{S}}-\mathrm{1}\end{array}$$

To calculate the probability of failure with FORM, the factor of safety needs to be evaluated during each iteration with D-Geo Stability. An experimental version of D-Geo Stability with an additional piece of software from the same developers called the probabilistic toolkit (PTK) was utilized to automatically execute D-Geo Stability with updated parameters calculated by the FORM algorithm in the PTK.

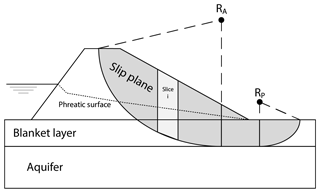
Figure D1 Schematization of the slip plane and phreatic surface used for the macro stability calculation.

The iterative procedure of finding the critical slip plane is both computationally demanding and complicates conversion in the probabilistic FORM algorithm. To speed up the procedure in the computation, first, a test run is performed using average soil strength parameters at a fixed critical slip plane with a water level halfway at the crest. With the results of the first indicative run, stochastic variables with little to no influence ($\left|\mathit{\alpha }\right|<\mathrm{0.001}$) are set as constants. Then the entire model was run for each discretized water level.

After the run the fragility curve was checked for points where no convergence was achieved with FORM or a non-critical slip circle must have been evaluated. To this end, points where the maximum number of iterations was reached or the probability of failure decreased with ascending water level were removed to obtain a monotonically increasing fragility curve.

Appendix E: FORM algorithm

The first-order reliability method (FORM) is a method to iteratively calculate the probability of a limit state function (Z(X)≤0) being exceeded given a set of independent random variables (X) (Hasofer and Lind, 1974). The starting point for the iteration is arbitrary, but usually the mean of the variables is taken as the first point to evaluate (x^∗). The problem is first simplified by converting the random variables before each iteration into realizations of equivalent normally distributed variables (x^′) with an equivalent normal transformation (Rackwitz and Flessler, 1978).

$$\begin{array}{}\text{(E1)}& {\displaystyle }& {\displaystyle }{{\mathit{\mu }}^{\prime }}_{X_i}=x_i^{\ast }-{{\mathit{\sigma }}^{\prime }}_{X_i}\times {\mathrm{\Phi }}^{-\mathrm{1}}\left[F\left(x_i^{\ast }\right)\right]\text{(E2)}& {\displaystyle }& {\displaystyle }{{\mathit{\sigma }}^{\prime }}_{X_i}={\displaystyle \frac{\mathit{\phi }\left\{{\mathrm{\Phi }}^{-\mathrm{1}}\left[F\left(x_i^{\ast }\right)\right]\right\}}{f\left(x_i^{\ast }\right)}},\end{array}$$

where ${{\mathit{\mu }}^{\prime }}_{X_i}$ and ${{\mathit{\sigma }}^{\prime }}_{X_i}$ are the mean and standard deviation of the equivalent normal distribution of variable x_i in the point x^∗. Also, f and F are the probability density function (PDF) and cumulative distribution function (CDF) of variable x_i, while φ and Φ are the standard normal PDF and CDF.

The mean and standard deviation of the limit state function are evaluated by

$$\begin{array}{}\text{(E3)}& {\displaystyle }& {\displaystyle }{\mathit{\mu }}_Z=Z\left(x^{\ast }\right)+\sum _{i=\mathrm{1}}^n{\displaystyle \frac{\partial Z}{\partial X_i}}(\mathit{\mu }{{}^{\prime }}_{X_i}-x_i^{\ast })\text{(E4)}& {\displaystyle }& {\displaystyle }{\mathit{\sigma }}_Z=\sqrt{\sum _{i=\mathrm{1}}^n{\left({\displaystyle \frac{\partial Z}{\partial X_i}}\right)}^{\mathrm{2}}{{\mathit{\sigma }}_{X_i}^{\prime }}^{\mathrm{2}}}.\end{array}$$

With the mean and standard deviation calculated from the design point (x^∗), the reliability index (β) and influence factor of each variable (${\mathit{\alpha }}_{X_i})$ are calculated.

$$\begin{array}{}\text{(E5)}& {\displaystyle }& {\displaystyle }\mathit{\beta }={\displaystyle \frac{{\mathit{\mu }}_Z}{{\mathit{\sigma }}_Z}}\text{(E6)}& {\displaystyle }& {\displaystyle }{\mathit{\alpha }}_{X_i}={\displaystyle \frac{\partial Z}{\partial X_i}}\times {\displaystyle \frac{{\mathit{\sigma }}_{X_i}^{\prime }}{{\mathit{\sigma }}_Z}}\end{array}$$

The point is updated by adjusting each variable based on the overall safety level (β) and the sensitivity of the limit state to the variable (${\mathit{\alpha }}_{X_i})$:

$$\begin{array}{}\text{(E7)}& {\displaystyle }{x}_i^{\ast }=\mathit{\mu }{{}^{\prime }}_{X_i}-{\mathit{\alpha }}_{X_i}\mathit{\beta }{{\mathit{\sigma }}^{\prime }}_{X_i}.\end{array}$$

The process is repeated until the reliability index has converged and no longer changes significantly after an iteration.

While the method is effective, there are limitations. It is not guaranteed that FORM finds the design point with the highest probability but rather converges to a local design point. Furthermore, for FORM to converge, the limit state function should be smooth without jumps or discontinuities. This complicated the implementation of, for example, macro stability, as when a different slip circle becomes critical, there can be a sudden jump in the evaluation of the limit state function.