the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
High-spatial-resolution probability maps of drought duration and magnitude across Spain
Fernando Domínguez-Castro
Sergio M. Vicente-Serrano
Miquel Tomás-Burguera
Marina Peña-Gallardo
Santiago Beguería
Ahmed El Kenawy
Yolanda Luna
Ana Morata
Assessing the probability of occurrence of drought is important for improving current drought assessment, management and mitigation measures, and strategies across Spain. This study employed two well-established drought indices, the Standardized Precipitation Index (SPI) and the Standardized Precipitation Evapotranspiration Index (SPEI), to characterize drought duration and magnitude at different timescales over Spain. In order to map the drought hazard probability, we applied the extreme value theory and tested different thresholds to generate peak-over-threshold (POT) drought duration and magnitude series. Our results demonstrate that the generalized Pareto (GP) distribution performs well in estimating the frequencies of drought magnitude and duration. Specifically, we found a good agreement between the observed and modelled data when using upper percentiles to generate the POT series. Spatially, our estimations suggest a higher probability of extreme drought events in southern and central Spain compared to the northern and eastern regions. Also, our study found spatial differences in drought probability estimations as a function of the selected drought index (i.e. SPI vs. SPEI) and timescale (i.e. 1, 3, 6, and 12 months). Drought hazard probability maps can contribute to the better management of different sectors (e.g. agriculture, water resources management, urban water supply, and tourism) at national, regional, and even local scale in Spain.
- Article
(13309 KB) - Full-text XML
-
Supplement
(3882 KB) - BibTeX
- EndNote
Drought is one of the main hydroclimatic hazards in Spain, with adverse impacts on natural and human environments (Pérez and Barreiro-Hurlé, 2009; UNEP, 2006). Numerous studies have analysed drought characteristics in Spain, suggesting a strong variability over both space and time (e.g. Domínguez-Castro et al., 2019a; González-Hidalgo et al., 2018). In Spain, drought management measures are usually based on insurance and government subsidies to diminish their impacts, particularly those related to the agricultural sector (Fernández, 2006). Alongside the existing systems for monitoring hydrological drought conditions across Spain (Maia and Vicente-Serrano, 2017), there are various pieces of national legislation (e.g. special drought plans) that aim at improving drought adaptation strategies and practices (Garrick et al., 2017).
Although current national measures are quite useful to diminish drought risk, other improved approaches are still desired to reduce drought risk, particularly for real-time drought monitoring (e.g. Svoboda et al., 2002) and forecasting (e.g. Mishra et al., 2009; Mishra and Singh, 2011). In this context, drought probability maps can be a promising tool to characterize drought risk at a detailed spatial scale. In particular, it is possible to determine the probability of drought episodes of a certain severity, allowing for better sectorial management strategies. Due to the availability of dense spatial climate data, there is a possibility to map drought probability at a fine spatial scale. This detailed scale can be useful for different socioeconomic sectors and for natural ecosystems. The utility of probabilistic approaches for enhancing drought monitoring and adaptation was evidenced in many regions worldwide (e.g. Engeland et al., 2005; Hussain et al., 2018; She et al., 2014; Tosunoglu and Can, 2016; Zamani et al., 2015).
In Spain, several studies have developed dry spell probability maps (e.g. Lana et al., 2006; Martin-Vide and Gomez, 1999; Pérez-Sánchez and Senent-Aparicio, 2018). However, given that the probability of occurrence of dry spells is higher in arid regions than in humid regions, these studies did not account for the different drought hazard probabilities across Spain. It is well-recognized that the frequency and duration of dry spells are largely driven by the climatology of the studied area. Accordingly, the spatial variability of climate aridity can show similar spatial patterns to those of dry spell probability. However, drought probability cannot necessarily be related to the spatial patterns of climate aridity, as it can be associated more with the intrinsic characteristics of drought events. This is simply because, irrespective of the climatology, drought can occur in any world region when there is a negative anomaly with respect to the long-term average moisture conditions (Wilhite and Pulwarty, 2017). This highlights the importance of data standardization to make drought characteristics (e.g. duration, intensity, severity) comparable among regions with different climatic conditions. Several drought indices (e.g. Standardized Precipitation Index (SPI), Standardized Precipitation Evapotranspiration Index (SPEI), Palmer Drought Severity Index, Self-calibrated Palmer Drought Severity Index) have been developed to characterize drought conditions across regions with different climatic conditions (Redmond, 2002). Also, irrespective of climatic conditions, these indices can identify drought episodes according to their duration and magnitude (Dracup et al., 1980) Overall, based on these drought indices, the probability of occurrence of drought duration and magnitude can be characterized at a detailed spatial resolution. In their assessment of drought characteristics in Serbia, Tošić and Unkašević (2014) analysed the probability of occurrence of drought using the SPI between 1949 and 2011, concluding that the generalized Pareto (GP) distribution fits well with the series at 1- and 12- month timescales. Similarly, Yusof et al. (2013) analysed the probability of drought duration and magnitude using the SPI and rainfall data from 30 rain gauges distributed across peninsular Malaysia. Also, Zin et al. (2013) assessed the return period of drought severity over peninsular Malaysia by means of the SPI. An inspection of these studies reveals that they employed only an individual drought index in most cases, with few attempts to explore the possible differences in drought hazard probability as a function of different drought indices (e.g. Yan et al., 2018) or different drought timescales (Moradi et al., 2011; Tošić and Unkašević, 2014). Due to the varying response of the different hydrological subsystems, socioeconomic sectors, and natural ecosystems to drought, the impacts of droughts should be assessed at various drought timescales (McKee et al., 1993; Vicente-Serrano, 2013). Moreover, the spatial patterns of drought and hazard probability maps can differ largely in response to timescale (Vicente-Serrano, 2006). Taken together, it is important to assess drought hazard probability at different drought timescales to meet the specific needs of different socioeconomic sectors and natural systems.
The overall objective of this study is to employ a newly developed high-resolution spatial (1.21 km2) and temporal (weekly) gridded dataset of drought indices (Vicente-Serrano et al., 2017) to characterize drought events in Spain. Specifically, this study aims to (i) apply the extreme value theory to determine the best threshold and statistical distribution to fit the probability of drought duration and magnitude, (ii) explore spatial variations in this probability as a function of two common drought indices, with different underlying calculations (i.e. SPI vs. SPEI), and (iii) assess whether there are spatial differences in drought hazard probability in response to the different drought timescales. In Spain, this detailed spatial assessment is still lacking, limiting the possibility to provide guidance on the use of drought hazard probability to manage and mitigate drought risks at the national, regional, and even local scale.
2.1 Dataset
Based on gridded datasets of maximum and minimum air temperatures (1304 observatories), precipitation (2269 observatories), wind speed (82 observatories), relative humidity (179 observatories), and sunshine duration (112 observatories), Vicente-Serrano et al. (2017) developed a high-resolution spatial (1.21 km2) and temporal (weekly) drought dataset for Spain (412 178 pixels). This dataset spans the period from 1961 to 2014. This drought dataset was developed after a rigorous procedure to check the quality and homogeneity of the input climatic data. The grid of each variable was computed by a universal kriging method (Borrough and McDonnell, 1998; Pebesma, 2004) using the latitude, longitude, and elevation of each grid cell as auxiliary variables. The grid layers were validated with a jackknife resampling procedure (Phillips et al., 1992), indicating low differences between the predicted and the observed values for each grid. A detailed description of this dataset can be found in Vicente-Serrano et al. (2017). Overall, these gridded climatic data were employed to compute the SPI (McKee et al., 1993) and the SPEI (Vicente-Serrano et al., 2010) at different timescales ranging from 1 to 48 months (http://monitordesequia.csic.es, last access: 6 March 2019). While the SPI accounts only for precipitation data, the SPEI is based on a normalization of the difference between precipitation and atmospheric evaporative demand (AED). In this study, we employed these two drought indices to characterize the possible impacts of the AED on drought hazard probability. Drought characteristics were assessed for the period 1961–2014 using the SPI and SPEI at timescales of 1, 3, 6, and 12 months.
2.2 Selection of drought events
There are several criteria (thresholds) to identify independent drought events (e.g. Fleig et al., 2006; Lee et al., 1986). These thresholds are generally arbitrary, with no clear objective metrics to relate a certain value of a drought index with specific sectorial impacts. Indeed, this is a challenging task, given the large number of economic sectors and environmental systems impacted by droughts (Pérez and Barreiro-Hurlé, 2009). Furthermore, regions and sectors can respond differently to various drought timescales (Lorenzo-Lacruz et al., 2013; Pasho et al., 2012). In this work, we obtained series of drought events from weekly gridded series of SPEI and SPI at four selected timescales (1, 3, 6, and 12 months). We used a zero threshold to define drought events. Although this threshold allows for the inclusion of less severe drought events, it can secure a sufficient sampling size to conduct the probabilistic analysis. Importantly, the retention of drought events in this manner will not bias the obtained results, considering that high values of the series will be retained following the peak-over-threshold approach.
Overall, each drought event was defined as the period of consecutive weeks with SPI or SPEI values lower than zero. Likewise, the series of drought duration and magnitude were created based on the consecutive weeks of SPEI–SPI values below zero. The drought magnitude was calculated following the classical approach of Dracup et al. (1980). However, for operational purposes, the total magnitude of drought was transformed to positive values.
2.3 Probabilistic analysis
The peak-over-threshold (POT) series were obtained using series of drought duration and magnitude calculated at 1-, 3-, 6-, and 12-month timescales. These series are stationary and do not show any trend (Domínguez-Castro et al., 2019a), which is a prerequisite for the application of extreme value theory. The POT series were obtained according to a threshold (x0) as
In order to assess the role of the selected threshold in fitting the probability distribution of the series, we tested different thresholds defined according to the percentiles of the series (i.e. 0th, 10th, 20th, …, 90th, and 95th). Following this procedure, we selected the optimal percentile threshold to define the exceedance series of drought duration and magnitude for the different indices and timescales.
Numerous studies employed the GP distribution to model meteorological and hydrological droughts (e.g. Fleig et al., 2006; Nadarajah, 2008; Nadarajah and Kotz, 2008; Chen et al., 2011; Yusof et al., 2013; Tošić and Unkašević, 2014; Trenberth et al., 2014; Zamani et al., 2015; Liu et al., 2016). This is mainly because the probability distribution of a POT series, with random occurrence times, fits well with GP distribution (e.g. Hosking and Wallis, 1987; Pham et al., 2014; Wang, 1991). The GP distribution is a flexible, long-tailed distribution, whose distribution function is formulated as
where κ, α, and ε are the shape, scale, and location parameters of the distribution origin that correspond to the lower bound x0. The GP parameters were obtained using L-moment statistics following Hosking (1990).
Hosking (1990) proposed a procedure to provide parametric approximations to the relationships between L skewness and L kurtosis. This procedure allows for the determination of the suitability of the GP distribution to fit the exceedance obtained from different x0 values. Herein, we plotted the different L-moment diagrams with the statistics obtained from drought duration and magnitude series. The aim was to assess the suitability of the different x0 thresholds to obtain POT series with a good fit to the GP distribution.
We applied the Anderson–Darling test to check the goodness of fit of the POT series obtained from different x0 thresholds. To define the most suitable threshold, we paid attention to securing a sample of sufficient length to obtain solutions for the GP parameters. This is important to obtain reliable probability estimations. For this purpose, we compared the observed maximum drought duration and magnitude obtained for the whole study period (1961–2014) with those estimated using GP distribution and POT for the different thresholds. Then, we calculated the probability that an event of magnitude XT in a period of T=54 years (expressed in the original scale) will occur at least once in a period of T years. This is formulated as
where λ is a frequency parameter equalling the average number of occurrences of X per year in the original sample. The performance of each threshold was assessed using different accuracy statistics, including the mean absolute error (MAE), the Willmott D agreement index (Willmott, 1981), and the Pearson's r correlation coefficient. Comparisons were made for the observed maximum drought duration and magnitude and the GP estimations for the same sample length.
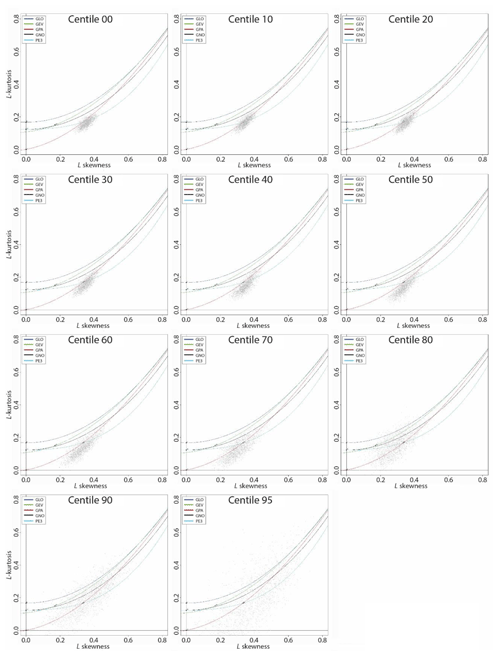
Figure 1L-moment diagrams for the peak-over-threshold series obtained from the 1-month SPEI duration series.
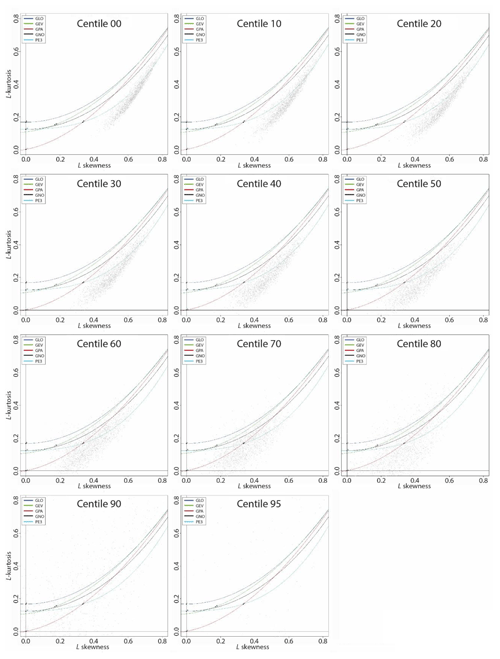
Figure 2L-moment diagrams for the peak-over-threshold series obtained from the 12-month SPEI magnitude series.

Figure 3Probability density diagrams showing the number of cases corresponding to the peak-over-threshold drought duration–magnitude series at different percentiles and different timescales (1, 3, 6, and 12 months) using (a) SPI and (b) SPEI.
Once a general threshold was established to define the POT series of drought duration and magnitude, we determined the goodness of the GP modelling for each drought index and timescale. For this purpose, we used probability–probability (P–P) plots, which define the extent to which the empirical and modelled GP cumulative distribution functions (CDFs) closely match. This procedure was applied to a total of 412 178 gridded series of drought magnitude and duration covering the four selected timescales of the SPI and SPEI. The empirical CDFs were obtained using the plotting position formula proposed by Hosking (1990) for highly skewed data, according to
where i is the rank of the observations arranged in descending order, and N is the number of observations. The goodness of agreement between the empirical and modelled CDFs was tested using a weighted correlation coefficient. This procedure gives more weight to the highest and less frequent observations in the sample, which are more relevant to extreme value analysis. The weight was defined using the empirical CDF as
where CDF is the cumulative distribution function, and j refers to the observations in the series of exceedance sorted in ascending order.
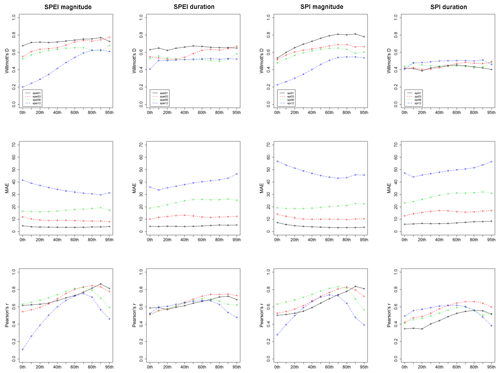
Figure 4Willmott's D, mean absolute error (MAE), and Pearson's r summarized as a function of the different percentiles used to obtain the peak-over-threshold series. All accuracy metrics were computed based on comparing the maximum observed and modelled 1-, 3-, 6-, and 12-month SPI and SPEI drought duration and magnitude between 1961 and 2014. The modelled data were computed using the generalized Pareto distribution.
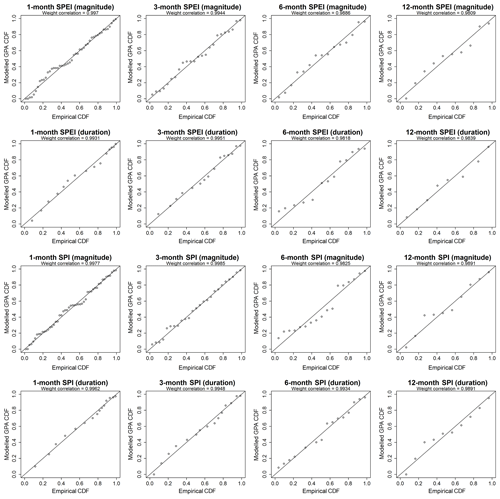
Figure 5Example of probability–probability (P–P) plots for the series of 1-, 3-, 6-, and 12-month SPEI and SPI drought duration and drought magnitude obtained by means of the 80th percentile used as a threshold to derive the peak-over-threshold series.
3.1 Selection of the distribution and threshold to define the POT series
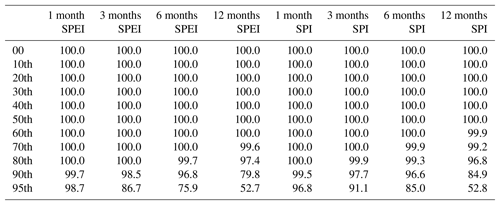
Figure 1 illustrates some examples of L-moment diagrams, considering the 1-month SPEI duration series over peninsular Spain. The series for each diagram were obtained considering POT at different percentiles. Each line represents a theoretical curve distribution: the generalized logistic (GLO, blue), generalized extreme value (GEV, green), generalized Pareto (GPA, red), generalized normal (GNO, black), and Pearson type III (PE3, light blue). As noted, irrespective of the selected threshold, the drought duration series tend to closely approximate to the GP distribution. Notably, there is a higher dispersion of points around the theoretical curve at higher percentiles, which can simply be seen in the context of lower sampling size. Figure 2 depicts the L-moment diagrams corresponding to the 12-month SPEI magnitude series. The plots show high dispersion considering the different percentile thresholds. Nevertheless, at low percentiles, the points do not approximate to the theoretical curve of the GP distribution, but they conversely tend to approximate to the GP curve at percentiles between 60th and 80th. Again, the points exhibited high dispersion at upper percentiles (mostly above the 85th). An inspection of Figs. S1 to S14 in the Supplement suggests similar patterns for other timescales and for the drought duration and magnitude series obtained using the SPI. Table 1 summarizes the percentage of the POT series that fit well with the GP distribution following Anderson–Darling statistics. As listed, the series of drought magnitude show a better fit to GP distribution than those of drought duration, but with no considerable differences between SPI and SPEI. In contrast, we noted remarkable differences amongst the different timescales. For example, we noted that a high percentage of the series obtained for low percentiles did not fit well to the GP distribution. In contrast, for all drought duration and magnitude series, this fitting improved markedly when considering higher percentiles (mostly above the 40th percentile). The only exceptions were found for the duration series obtained at a 1-month timescale, but considering thresholds higher than the 80th percentile either for SPI or SPEI. The total percentage of these series is close to 100 %. Overall, although the results suggest that high percentiles (e.g. 90th or 95th) were more appropriate to define the series of drought duration and magnitude, our decision was to define the series using a more relaxed threshold (80th percentile). This decision was motivated mainly by the notion that L-moment statistics showed high dispersion at the uppermost percentiles. Furthermore, it was quite difficult to secure a sufficient sampling size using these upper percentiles. Figure 3 shows the number of drought events corresponding to the different percentiles and timescales (i.e. 1, 3, 6, and 12 months). It can be noted that the number of events using the 90th and 95th percentile thresholds was very low for all timescales. This low number of events was statistically insufficient for the reliable estimation of L-moment and GP parameters (Table 2). Accordingly, we considered lower percentiles to get more reliable probabilistic estimations. In this context, our results indicated that the series of drought duration and magnitude obtained using the 80th percentile as a threshold mostly fit to the GP distribution, and the majority of these series (≈99 %) showed solutions for GP parameters. Figure 4 depicts the accuracy metrics (i.e. Willmott's D, MAE, and Pearson's r coefficient), which compare the maximum observed and modelled drought duration and magnitude for each grid. It can be noted that the agreement between the maximum observed and modelled values is higher for drought magnitude series than for drought duration series. However, for drought magnitude and duration series, this agreement improved when considering higher percentiles, especially the 80th percentile. These findings were clearly evident for the SPI and SPEI and for all timescales.
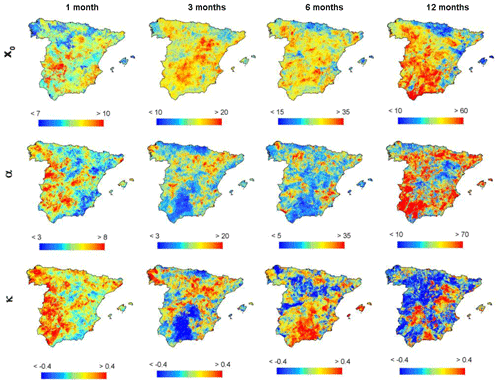
Figure 7Spatial distribution of the parameters of the GP distribution calculated for the SPI duration series.
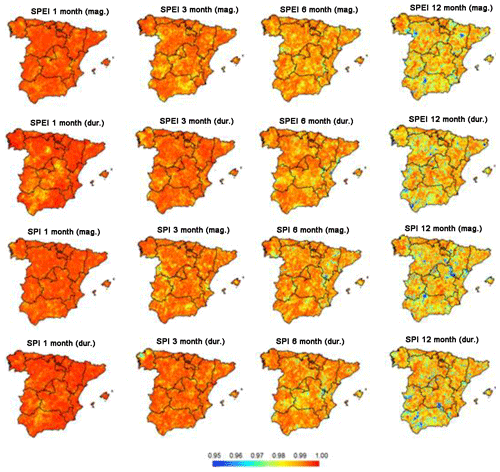
Also, we compared the empirical and modelled cumulative distribution functions using the GP distribution considering the 80th percentile POT series. Comparisons were made at the pixel scale considering the two drought indices (SPI vs. SPEI) and the different timescales. A representative example is shown in Fig. 5 for the grid point located at 40∘ N and 3∘ W. As illustrated, we noted a high agreement between the empirical and modelled CDFs, irrespective of the drought index and the timescale. However, a lower agreement was observed for longer timescales (i.e. 6 and 12 months). This can be expected given the low sampling size at long timescales in comparison to shorter timescales. Overall, the weighted correlations between the empirical and the modelled CDFs showed high values (>0.98) in all cases, which was reflected in the general observed pattern for the whole of Spain. Figure 6 depicts the spatial distribution of the weighted correlations between the empirical and the GP-distribution-modelled CDFs using the 80th percentile POT series. At the 1- and 3-month timescales, the correlations were close to 1 for all of Spain. The magnitude of correlation decreased for the 6- and 12-month timescales, despite being above 0.97 in most areas. Overall, these findings support our decision to select the 80th percentile and the GP distribution to statistically model drought duration and magnitude in our study domain.
3.2 Mapping drought duration and magnitude
Figures 7 and 8 illustrate the spatial distribution of GP parameters calculated for drought duration series obtained using the SPI and SPEI, respectively. The GP parameters showed very similar distributions for SPI and SPEI. However, we found considerable spatial variations in the distribution of these parameters as a function of the drought timescale, with higher values of the location (Xo) and scale (α) parameters for longer timescales. This can be explained by the increase in drought duration at longer timescales. The shape (k) parameter exhibited similar range values for all timescales. Herein, it is difficult to interpret the geographical distribution of the shape (k), as there is large uncertainty in estimating this parameter (Rosbjerg et al., 1992). As illustrated in Figs. S15 and S16, all parameters showed similar spatial patterns for the drought magnitude series.
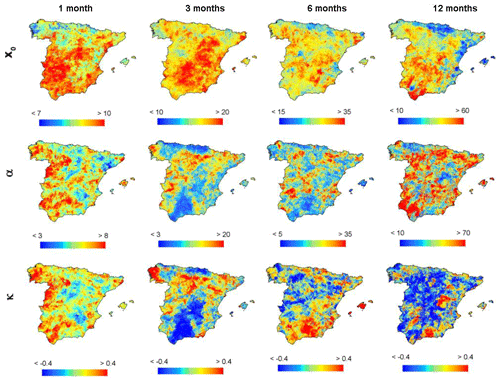
Figure 8Spatial distribution of the parameters of the GP distribution calculated for the SPEI duration series.
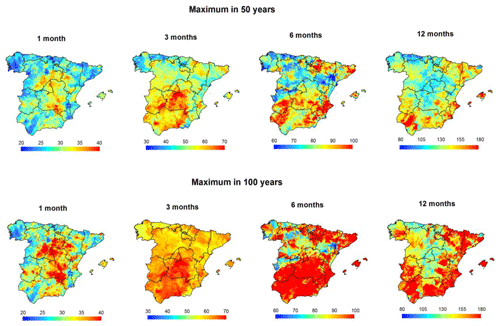
We mapped drought probability for the drought duration and magnitude series using parameter maps and Eq. (3). Figure 9 shows the estimated drought duration (in weeks) obtained from the 1-, 3-, 6-, and 12-month SPEI series for periods of 50 and 100 years. The results suggest important spatial differences among drought timescales. For example, at the 1-month timescale, the maximum duration was found in the central areas of Spain, with more than 40 weeks of consecutive negative SPEI values. A similar pattern can also be noted for the 3-month timescale, as central and southern Spain experience a longer duration. In northern Spain, the estimated maximum drought duration is almost half that in central Spain. Nevertheless, the spatial patterns of drought probability differ markedly at the timescales of 6 and 12 months, with the maximum duration recorded in south-eastern and south-western regions and parts of northern and north-eastern Spain. The spatial patterns found at the 12-month timescale closely resemble those observed at the 6-month timescale, suggesting a maximum drought duration (>180 weeks) in a period of 50 years over some regions in the south-west and along the eastern Mediterranean coast. On the other hand, considering the maximum drought duration for a period of 100 years, drought events are expected to extend spatially, especially in southern Spain. Figure 10 reveals that drought probability maps obtained using SPI are similar to those obtained using SPEI, although with some spatial differences that can mainly be linked to drought timescale. Figure 11 summarizes the relationship between the maximum drought duration of SPEI and SPI, considering 1-, 3-, 6-, and 12-month timescales and periods of 50 and 100 years. For drought duration, the agreement between SPI and SPEI is stronger considering long timescales. For timescales between 1 and 6 months, the SPEI tends to record higher quantile estimates than SPI. Nevertheless, at the 12-month timescale, the differences in the quantile estimates between the two indices are clearly minimized. For drought magnitude, the quantile estimates show more consistent spatial patterns for the two indices compared to those identified for drought duration series (Figs. S17 to S19).
We developed high-resolution drought probability maps for Spain using two widely recognized drought indices that are spatially and temporally comparable: the Standardized Precipitation Index (SPI) and the Standardized Precipitation Evapotranspiration Index (SPEI). Although they have similar conceptual backgrounds, these indices differ in their input variables. Specifically, while the SPI accounts only for precipitation data (McKee et al., 1993), the SPEI considers the atmospheric evaporative demand (AED) in its calculation (Vicente-Serrano et al., 2010). In this study, we computed these two drought indices at different timescales (1, 3, 6, and 12 months). The aim was to assess whether there are noticeable spatial differences in the obtained drought hazard probabilities as a function of the selected index and/or timescale.
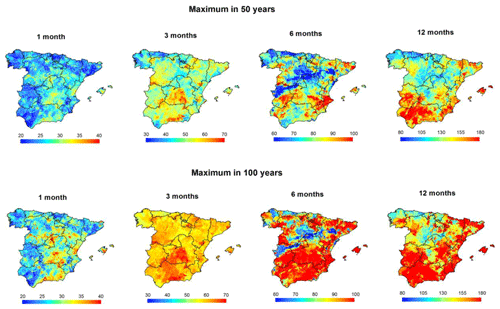
Figure 10Spatial distribution of the maximum drought duration (in weeks) from the 1-, 3-, 6-, and 12-month SPI series in a period of 50 and 100 years.
We assessed the suitability of the GP distribution to model drought duration and magnitude events. The results demonstrate that drought magnitude and duration series mostly fit well with a GP distribution, a finding that was confirmed in earlier drought assessment investigations in many regions worldwide (e.g. Chen et al., 2011; Serra et al., 2016; Vicente-Serrano and Beguería-Portugués, 2003; Zamani et al., 2015). In this study, our decision to select the GP distribution was motivated by the need to achieve a balance between the goodness of the fit to the GP distribution on the one hand and the selection of a representative threshold to obtain the POT series on the other hand. Our exploratory analysis suggests the use of the 80th percentile as a threshold. This threshold is a good balance between the two requirements for the SPI and SPEI and for all timescales.
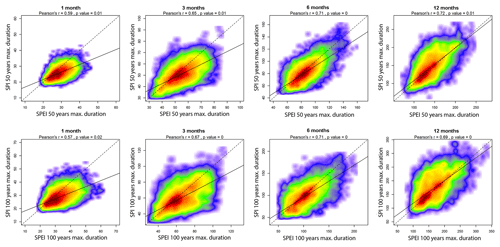
Figure 11Scatterplots showing the relationship between the maximum drought duration (in weeks) expected in a period of 50 and 100 years considering 1-, 3-, 6-, and 12-month SPEI and the SPI. The colours represent the density of points, with red denoting the highest density. Given the large sample used, the significance of the Pearson's r coefficients was estimated by means of a Monte Carlo approach using 103 random samples, with each sample containing 30 cases.
Table 1Percentage of the peak-over-threshold drought duration and magnitude series that fit well with the generalized Pareto distribution following Anderson–Darling statistics. Results are summarized for different percentiles and timescales using SPEI and SPI.
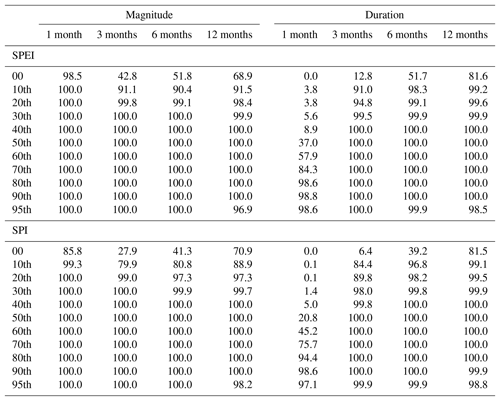
Table 2Percentage of cases in which the solution for the L moment and the generalized Pareto distribution parameters is found for the peak-over-threshold drought duration–magnitude series at different percentiles from 1-, 3-, 6-, and 12-month SPI and SPEI.
In earlier hydrologic and climatic hazards investigations, a regionalization approach has been employed to estimate the probability distribution, L-moment statistics, and distribution parameters (e.g. Durrans and Tomic, 1996; Serra et al., 2016; She et al., 2014). As opposed to these studies, our preference was given to analyse hazard probability locally. Specifically, to calculate the L-moment statistics and the distribution parameters, we considered each gridded cell as an independent series. While regionalization is advantageous in terms of spatial homogeneity and the reduction of parameter uncertainty (Hosking and Wallis, 1997), characterization of drought conditions in our study domain reveals noticeable spatial differences in response to drought timescale. This is clearly evident for probabilities of both drought duration and magnitude. Regionalization is usually based on the variables used for calculating drought indices (i.e. precipitation or the difference between precipitation and atmospheric evaporative demand) (Ghosh and Srinivasan, 2016; Habibi et al., 2018; Santos et al., 2011; Yuan et al., 2013; Zhang et al., 2015). Importantly, this study stresses that this kind of regionalization might not be useful when drought hazard differs strongly due to drought timescale. Previous studies indicated that the spatial patterns of drought may differ strongly as a function of drought timescale, especially with different temporal influences of local–regional precipitation events on drought index values (e.g. Vicente-Serrano, 2006). This is confirmed in our study for the whole of Spain, where the spatial patterns of the GP parameters and the maps of hazard probability strongly vary due to the different drought timescale. Again, this stresses the difficulty of applying regionalization approaches to obtain maps of drought probability. This difficulty is confirmed in this study, as our findings reveal differences in drought probability as a consequence of the selected drought index, which makes this kind of regionalization a challenging task. A possible solution could be establishing different regionalization schemes based on the different series of drought indices and timescales. However, this is practically disadvantageous, as it makes the use of probability estimations by end users more confusing (e.g. stakeholders, decision makers, and local communities). Also, with the spatial coherence and the observed gradients of GP parameters, a direct calculation of hazard probabilities at the local scale is highly recommended, particularly in regions with strong spatial and temporal climatic variability like Spain. Overall, taking all these limitations into consideration, this study stresses that employing regionalization approaches to determine drought hazard probabilities should be done with caution, especially when different drought indices and timescales are used.
Assessing the different spatial patterns of drought probabilities as a function of timescales has strong implications for drought impact assessment and drought mitigation. It is well-established that different hydrological, agricultural, and environmental systems respond differently to drought timescales (Pasho et al., 2012; Peña-Gallardo et al., 2018; Vicente-Serrano, 2013). As such, for more effective assessment and monitoring of drought hazard, drought timescales must be linked to specific drought impacts. This is basically because although drought probability can differ in response to drought timescale, the impacts of drought hazard may vary considerably from one region to another due to different environmental and socioeconomic factors. Correspondingly, the degree of vulnerability can differ according to drought timescale and region. For example, although with the high probability of occurrence of an extreme drought event at a certain timescale in a particular region, drought risk may be small if the sensitivity to drought timescale is low. This confirms that it is essential to obtain drought hazard probability maps at different timescales. Practically, the real hazard would be definitely derived from a drought timescale that triggers impacts in a given space and sector.
Recently, there has been a great debate on the influence of climate change processes on drought severity (Dai, 2013; Sheffield et al., 2012; Trenberth et al., 2014). This debate is largely motivated by the role of warming processes and the atmospheric evaporative demand in drought severity. Numerous studies have shown a noticeable increase in the AED across the Mediterranean region, which could enhance the severity of drought events in comparison to events driven mainly by precipitation deficit (Stagge et al., 2017; Vicente-Serrano et al., 2014). Here, we indicated that, mainly at timescales from 1 to 6 months, SPEI duration and magnitude values are higher than those of the SPI. This finding suggests that the increased AED due to warming processes may have a certain role in increasing drought duration and magnitude hazard probabilities in Spain. When a drought event occurs as a consequence of a precipitation deficit, high values of the AED can increase the magnitude and duration of drought events. However, this pattern was not observed for long drought timescales (i.e. 12 months), which showed small differences between the SPI and SPEI drought duration and magnitude quantile maps. This could be explained by the strong seasonality that characterizes the climate of Spain. This can be seen for the 12-month timescale, which summarizes the annual climate conditions. As indicated by Vicente-Serrano et al. (2014), the role of increased AED (mostly recorded during summer months) would be diminished in comparison to the role of precipitation. In contrast, the role of the AED would be more highlighted at shorter timescales that record stronger seasonal variability.
Assessing drought hazard probability by means of joint probabilities of drought duration and magnitude has been applied in more depth through the use of copulas (e.g. Ganguli and Reddy, 2012; Liu et al., 2011; Zhang et al., 2015). Nevertheless, given the nature of drought indices, the time series exhibit strong temporal autocorrelation, and accordingly the duration and magnitude of particular drought events can show high agreement. Here, we found a strong correlation between the magnitude and the duration of drought events for the selected drought indices and timescales. This indicates that – as expected – the total magnitude of an event is proportional to drought duration. Therefore, although copulas could give some additional information for particular events, we still believe that an accurate evaluation of drought hazard probability in Spain using a univariate approach is more advantageous.
Recalling the strong spatial differences in the drought hazard probability over Spain, the maps obtained in this study can contribute to better management practices for different sectors, including agriculture, water resources management, urban water supply, tourism, and environmental management. The spatial quantile probabilities developed in this study, combined with those estimated for 50 and 100 years, are fully accessible to the research community and end users via the web repository of the Spanish National Research Council (CSIC) (Domínguez-Castro et al., 2019b).
The Generalized Pareto parameters and drought risk maps developed in this study are accessible at http://digital.csic.es/handle/10261/178150 (Domínguez-Castro et al., 2019b).
The supplement related to this article is available online at: https://doi.org/10.5194/nhess-19-611-2019-supplement.
All the authors contributed equally to the paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Hydroclimatic extremes and impacts at catchment to regional scales”. It is not associated with a conference.
This work was supported by the following research projects: CGL2014-52135-C03-01
and PCIN-2015-220 financed by the Spanish Commission of Science and Technology
and FEDER, 1560/2015; Herramientas de monitorización de la
vegetación mediante modelización ecohidrológica en parques
continentales financed by the Red de Parques Nacionales; IMDROFLOOD financed
by Water Works 2014; a co-funded call of the European Commission and
INDECIS, which is part of ERA4CS; and an ERA-NET initiated by JPI Climate,
funded by MINECO with co-funding by the European Union (grant 690462).
Marina Peña-Gallardo was funded by the Spanish Ministry of Economy and
Competitiveness, Miquel Tomas-Burguera was supported by a doctoral grant by
the Spanish Ministry of Education, Culture and Sport, and Ahmed El Kenawy was
supported by a postdoctoral Juan de la Cierva contract.
Edited by: Chris Reason
Reviewed by: two anonymous referees
Borrough, P. A. and McDonnell, R. A.: Principles of Geographical Information Systems, Oxford University Press, Oxford, UK, 1998.
Chen, L.-H., Hong, Y.-T., and Hsu, C.-W.: A study on regional drought frequency analysis using self-organizing map and l-moments, J. Taiwan Agric. Eng., 57, 57–77, 2011.
Dai, A.: Increasing drought under global warming in observations and models, Nat. Clim. Change, 3, 52–58, https://doi.org/10.1038/nclimate1633, 2013.
Domínguez-Castro, F., Vicente-Serrano, S. M., Tomás-Burguera, M., Peña-Gallardo, M., Beguería, S., El Kenawy, A., Luna, Y., and Morata, A.: High spatial resolution climatology of drought events for Spain: 1961–2014, Int. J. Climatol., in review, 2019a.
Domínguez-Castro, F., Vicente-Serrano, S. M., Tomás-Burguera, M., Peña-Gallardo, M., Beguería, S., El Kenawy, A. M., Luna, Y., and Morata, A.: Generalized Pareto Parameters and maps of drought risk for Spain, Digital CSIC, http://digital.csic.es/handle/10261/178150, 2019b.
Dracup, J. A., Lee, K. S., and Paulson, E. G.: On the definition of droughts, Water Resour. Res., 16, 297–302, https://doi.org/10.1029/WR016i002p00297, 1980.
Durrans, S. R. and Tomic, S.: Regionalization of low-flow frequency estimates: An Alabama case study, J. Am. Water Resour. Assoc., 32, 23–37, 1996.
Engeland, K., Hisdal, H., and Frigessi, A.: Practical extreme value modelling of hydrological floods and droughts: A case study, Extremes, 7, 5–30, https://doi.org/10.1007/s10687-004-4727-5, 2005.
Fernández, A.: El sistema español de seguros agrarios, El Sect. Asegur. y los planes y fondos pensiones, 833, 87–99, 2006.
Fleig, A. K., Tallaksen, L. M., Hisdal, H., and Demuth, S.: A global evaluation of streamflow drought characteristics, Hydrol. Earth Syst. Sci., 10, 535–552, https://doi.org/10.5194/hess-10-535-2006, 2006.
Ganguli, P. and Reddy, M. J.: Risk Assessment of Droughts in Gujarat Using Bivariate Copulas, Water Resour. Manage., 26, 3301–3327, https://doi.org/10.1007/s11269-012-0073-6, 2012.
Garrick, D. E., Hall, J. W., Dobson, A., Damania, R., Grafton, R. Q., Hope, R., Hepburn, C., Bark, R., Boltz, F., De Stefano, L., O'Donnell, E., Matthews, N., and Money, A.: Valuing water for sustainable development, Science, 358, 1003–1005, https://doi.org/10.1126/science.aao4942, 2017.
Ghosh, S. and Srinivasan, K.: Analysis of Spatio-temporal Characteristics and Regional Frequency of Droughts in the Southern Peninsula of India, Water Resour. Manage., 30, 3879–3898, https://doi.org/10.1007/s11269-016-1396-5, 2016.
González-Hidalgo, J. C., Vicente-Serrano, S. M., Peña-Angulo, D., Salinas, C., Tomas-Burguera, M., and Beguería, S.: High-resolution spatio-temporal analyses of drought episodes in the western Mediterranean basin (Spanish mainland, Iberian Peninsula), Acta Geophys., 66, 381–392, 2018.
Habibi, B., Meddi, M., Torfs, P. J. J. F., Remaoun, M., and Van Lanen, H. A. J.: Characterisation and prediction of meteorological drought using stochastic models in the semi-arid Chéliff–Zahrez basin (Algeria), J. Hydrol. Reg. Stud., 16, 15–31, https://doi.org/10.1016/j.ejrh.2018.02.005, 2018.
Hosking, J. R. M.: L-moments: analysis and estimation of distributions using linear combinations of order statistics, J. Roy. Stat. Soc. Ser. B, 52, 105–124, 1990.
Hosking, J. R. M. and Wallis, J. R.: Parameter and quantile estimation for the generalized pareto distribution, Technometrics, 29, 339–349, https://doi.org/10.1080/00401706.1987.10488243, 1987.
Hosking, J. R. M. and Wallis, J. R.: Regional Frequency Analysis: An Approach Based on L-moments, Cambridge University Press, Cambridge, 1997.
Hussain, T., Bakouch, H. S., and Iqbal, Z.: A New Probability Model for Hydrologic Events: Properties and Applications, J. Agric. Biol. Environ. Stat., 23, 63–82, https://doi.org/10.1007/s13253-017-0313-6, 2018.
Lana, X., Martínez, M. D., Burgueño, A., Serra, C., Martín-Vide, J., and Gómez, L.: Distributions of long dry spells in the Iberian Peninsula, years 1951–1990, Int. J. Climatol., 26, 1999–2021, https://doi.org/10.1002/joc.1354, 2006.
Lee, K. S., Sadeghipour, J., and Dracup, J. A.: An Approach for Frequency Analysis of Multiyear Drought Durations, Water Resour. Res., 22, 655–662, https://doi.org/10.1029/WR022i005p00655, 1986.
Liu, C.-L., Zhang, Q., Singh, V. P., and Cui, Y.: Copula-based evaluations of drought variations in Guangdong, South China, Nat. Hazards, 59, 1533–1546, https://doi.org/10.1007/s11069-011-9850-4, 2011.
Liu, Y., Lu, M., Huo, X., Hao, Y., Gao, H., Liu, Y., Fan, Y., Cui, Y., and Metivier, F.: A Bayesian analysis of Generalized Pareto Distribution of runoff minima, Hydrol. Process., 30, 424–432, https://doi.org/10.1002/hyp.10606, 2016.
Lorenzo-Lacruz, J., Moŕan-Tejeda, E., Vicente-Serrano, S. M., and Ĺopez-Moreno, J. I.: Streamflow droughts in the Iberian Peninsula between 1945 and 2005: Spatial and temporal patterns, Hydrol. Earth Syst. Sci., 17, 119–134, https://doi.org/10.5194/hess-17-119-2013, 2013.
Maia, R. and Vicente-Serrano, S. M.: Drought planning and management in the iberian peninsula, in: Drought and Water Crises, CRC Press, Boca Raton, 481–506, 2017.
Martin-Vide, J. and Gomez, L.: Regionalization of peninsular Spain based on the length of dry spells, Int. J. Climatol., 19, 537–555, 1999.
McKee, T. B., Doesken, N. J., and Kleist, J.: The relationship of drought frequency and duration to time scales, in: Eighth Conf. Appl. Climatol., 17–22 January 1993, Anaheim, USA, 179–184, 1993.
Mishra, A. K. and Singh, V. P.: Drought modeling – A review, J. Hydrol., 403, 157–175, https://doi.org/10.1016/j.jhydrol.2011.03.049, 2011.
Mishra, A. K., Singh, V. P., and Desai, V. R.: Drought characterization: A probabilistic approach, Stoch. Environ. Res. Risk A., 23, 41–55, https://doi.org/10.1007/s00477-007-0194-2, 2009.
Moradi, H. R., Rajabi, M., and Faragzadeh, M.: Investigation of meteorological drought characteristics in Fars province, Iran, Catena, 84, 35–46, https://doi.org/10.1016/j.catena.2010.08.016, 2011.
Nadarajah, S.: Generalized Pareto models with application to drought data, Environmetrics, 19, 395–408, https://doi.org/10.1002/env.885, 2008.
Nadarajah, S. and Kotz, S.: The generalized Pareto sum, Hydrol. Process., 22, 288–294, https://doi.org/10.1002/hyp.6602, 2008.
Pasho, E., Camarero, J. J., and Vicente-Serrano, S. M.: Climatic impacts and drought control of radial growth and seasonal wood formation in Pinus halepensis, Trees – Struct. Funct., 26, 1875–1886, https://doi.org/10.1007/s00468-012-0756-x, 2012.
Pebesma, E. J.: Multivariable geostatistics in S: The gstat package, Comput. Geosci., 30, 683–691, 2004.
Peña-Gallardo, M., Vicente-Serrano, S. M., Domínguez-Castro, F., Quiring, S., Svoboda, M., Beguería, S., and Hannaford, J.: Effectiveness of drought indices in identifying impacts on major crops across the USA, Clim. Res., 75, 221–240, 2018.
Pérez, L. and Barreiro-Hurlé, J.: Assessing the socio-economic impacts of drought in the Ebro River Basin – Análisis de los efectos socioeconómicos de la sequía en la cuenca del Ebro, Spanish J. Agric. Res., 7, 269–280, 2009.
Pérez-Sánchez, J. and Senent-Aparicio, J.: Analysis of meteorological droughts and dry spells in semiarid regions: a comparative analysis of probability distribution functions in the Segura Basin (SE Spain), Theor. Appl. Climatol., 133, 1061–1074, https://doi.org/10.1007/s00704-017-2239-x, 2018.
Pham, H. X., Asaad, Y., and Melville, B.: Statistical properties of partial duration series: Case study of North Island, New Zealand, J. Hydrol. Eng., 19, 807–815, https://doi.org/10.1061/(ASCE)HE.1943-5584.0000841, 2014.
Phillips, D. L., Dolph, J., and Marks, D.: A comparison of geostatistical procedures for spatial analysis of precipitation in mountainous terrain, Agric. Meteorol., 58, 119–141, 1992.
Redmond, K. T.: The depiction of drought: A commentary, B. Am. Meteorol. Soc., 83, 1143–1147, https://doi.org/10.1175/1520-0477(2002)083<1143:TDODAC>2.3.CO;2, 2002.
Rosbjerg, D., Madsen, H., and Rasmussen, P. F.: Prediction in partialduration series with generalized Pareto-distributed exceedances, Water Resour. Res., 28, 3001–3010, 1992.
Santos, J. F., Portela, M. M., and Pulido-Calvo, I.: Regional Frequency Analysis of Droughts in Portugal, Water Resour. Manage., 25, 3537–3558, https://doi.org/10.1007/s11269-011-9869-z, 2011.
Serra, C., Lana, X., Burgueño, A., and Martínez, M. D.: Partial duration series distributions of the European dry spell lengths for the second half of the twentieth century, Theor. Appl. Climatol., 123, 63–81, https://doi.org/10.1007/s00704-014-1337-2, 2016.
She, D.-X., Xia, J., Zhang, D., Ye, A.-Z., and Sood, A.: Regional extreme-dry-spell frequency analysis using the L-moments method in the middle reaches of the Yellow River Basin, China, Hydrol. Process., 28, 4694–4707, https://doi.org/10.1002/hyp.9930, 2014.
Sheffield, J., Wood, E. F., and Roderick, M. L.: Little change in global drought over the past 60 years, Nature, 491, 435–438, https://doi.org/10.1038/nature11575, 2012.
Stagge, J. H., Kingston, D. G., Tallaksen, L. M., and Hannah, D. M.: Observed drought indices show increasing divergence across Europe, Sci. Rep., 7, 14045, https://doi.org/10.1038/s41598-017-14283-2, 2017.
Svoboda, M., LeComte, D., Hayes, M., Heim, R., Gleason, K., Angel, J., Rippey, B., Tinker, R., Palecki, M., Stooksbury, D., Miskus, D., and Stephens, S.: The drought monitor, B. Am. Meteorol. Soc., 83, 1181–1190, https://doi.org/10.1175/1520-0477(2002)083<1181:TDM>2.3.CO;2, 2002.
Tošić, I. and Unkašević, M.: Analysis of wet and dry periods in Serbia, Int. J. Climatol., 34, 1357–1368, https://doi.org/10.1002/joc.3757, 2014.
Tosunoglu, F. and Can, I.: Application of copulas for regional bivariate frequency analysis of meteorological droughts in Turkey, Nat. Hazards, 82, 1457–1477, https://doi.org/10.1007/s11069-016-2253-9, 2016.
Trenberth, K. E., Dai, A., Van Der Schrier, G., Jones, P. D., Barichivich, J., Briffa, K. R., and Sheffield, J.: Global warming and changes in drought, Nat. Clim. Change, 4, 17–22, https://doi.org/10.1038/nclimate2067, 2014.
UNEP: Geo Year Book 2006: An overview of our changing environment, Nairobi, 2006.
Vicente-Serrano, S. M.: Differences in spatial patterns of drought on different time scales: An analysis of the Iberian Peninsula, Water Resour. Manage., 20, 37–60, https://doi.org/10.1007/s11269-006-2974-8, 2006.
Vicente-Serrano, S. M.: Spatial and temporal evolution of precipitation droughts in Spain in the last century, in: Adverse Weather in Spain, edited by: Martínez, F. and Rodríguez, C. C.-L., AMV Ediciones, Madrid, Spain, 283–296, 2013.
Vicente-Serrano, S. M. and Beguería-Portugués, S.: Estimating extreme dry-spell risk in the middle Ebro valley (northeastern Spain): A comparative analysis of partial duration series with a general Pareto distribution and annual maxima series with a Gumbel distribution, Int. J. Climatol., 23, 1103–1118, https://doi.org/10.1002/joc.934, 2003.
Vicente-Serrano, S. M., Beguería, S., and López-Moreno, J. I.: A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index, J. Climate, 23, 1696–1718, https://doi.org/10.1175/2009JCLI2909.1, 2010.
Vicente-Serrano, S. M., Azorin-Molina, C., Sanchez-Lorenzo, A., Revuelto, J., López-Moreno, J. I., González-Hidalgo, J. C., Moran-Tejeda, E., and Espejo, F.: Reference evapotranspiration variability and trends in Spain, 1961–2011, Global Planet. Change, 121, 26–40, https://doi.org/10.1016/j.gloplacha.2014.06.005, 2014.
Vicente-Serrano, S. M., Tomas-Burguera, M., Beguería, S., Reig, F., Latorre, B., Peña-Gallardo, M., Luna, M. Y., Morata, A., and González-Hidalgo, J. C.: A High Resolution Dataset of Drought Indices for Spain, Data, 2, 22, https://doi.org/10.3390/data2030022, 2017.
Wang, Q. J.: The POT model described by the generalized Pareto distribution with Poisson arrival rate, J. Hydrol., 129, 263–280, https://doi.org/10.1016/0022-1694(91)90054-L, 1991.
Wilhite, D. and Pulwarty, R. S.: Drought and Water Crises: Integrating Science, Management, and Policy, CRC Press, Boca Raton, 2017.
Willmott, C. J.: On the validation of models, Phys. Geogr., 2, 184–194, https://doi.org/10.1080/02723646.1981.10642213, 1981.
Yan, G., Wu, Z., Li, D., and Xiao, H.: A comparative frequency analysis of three standardized drought indices in the poyang lake basin, china, Nat. Hazards, 91, 353–374, https://doi.org/10.1007/s11069-017-3133-7, 2018.
Yuan, X.-C., Zhou, Y.-L., Jin, J.-L., and Wei, Y.-M.: Risk analysis for drought hazard in China: A case study in Huaibei Plain, Nat. Hazards, 67, 879–900, https://doi.org/10.1007/s11069-013-0614-1, 2013.
Yusof, F., Hui-Mean, F., Suhaila, J., and Yusof, Z.: Characterisation of Drought Properties with Bivariate Copula Analysis, Water Resour. Manage., 27, 4183–4207, https://doi.org/10.1007/s11269-013-0402-4, 2013.
Zamani, R., Tabari, H., and Willems, P.: Extreme streamflow drought in the Karkheh river basin (Iran): probabilistic and regional analyses, Nat. Hazards, 76, 327–346, https://doi.org/10.1007/s11069-014-1492-x, 2015.
Zhang, Q., Qi, T., Singh, V. P., Chen, Y. D., and Xiao, M.: Regional Frequency Analysis of Droughts in China: A Multivariate Perspective, Water Resour. Manage., 29, 1767–1787, https://doi.org/10.1007/s11269-014-0910-x, 2015.
Zin, W. Z. W., Jemain, A. A., and Ibrahim, K.: Analysis of drought condition and risk in Peninsular Malaysia using Standardised Precipitation Index, Theor. Appl. Climatol., 111, 559–568, https://doi.org/10.1007/s00704-012-0682-2, 2013.