Forecasting landslide mobility using an SPH model and ring shear strength tests: a case study

Flow-like landslides, such as flow slides and debris avalanches, have caused serious infrastructure damage and casualties for centuries. Effective numerical simulation incorporating accurate soil mechanical parameters is essential for predicting post-failure landslide mobility. In this study, smoothed particle hydrodynamics (SPH) incorporating soil ring shear test results were used to forecast the long-runout mobility for a landslide on an unstable slope in China. First, a series of ring shear tests under different axial stresses and shear velocities were conducted to evaluate the residual shear strength of slip zones after extensive shear deformation. Based on the ring shear test results, SPH modeling was conducted to predict the post-failure mobility of a previously identified unstable slope. The results indicate that the landslide would cut a fire service road on the slope after 12 s and cover an expressway at the foot of that slope after 36 s. In the model, the landslide would finally stop sliding about 38 m beyond the foot of the slope after 200 s. This study extends the application of the SPH model from disaster simulations to predictive analysis of unstable landslide. In addition, two sets of comparative calculations were carried out which demonstrate the robustness of the SPH method.

1 Introduction

Flow-like landslides triggered by intense earthquakes or rainfall, such as debris and rock avalanches, have caused serious infrastructure damage and casualties for centuries (Wang et al., 2005; Okada et al., 2007). This kind of landslide is commonly high speed and has a long runout distance. For example, a large landslide in southern Italy in February 2010 had a runout distance of 1.2 km and necessitated the evacuation of nearly 2300 people. This landslide was triggered by heavy and prolonged rainfall between August 2009 and February 2010 (Gattinoni et al., 2012). The 2009 Shiaolin landslide in Taiwan, induced by a cumulative rainfall of nearly 1700 mm from Typhoon Morakot, buried Shiaolin Village and resulted in more than 400 people dead and missing (Tsou et al., 2011). Numerical simulations that incorporate accurate soil mechanical parameters are a powerful tool for simulating landslide runout distances; these simulations can provide fundamental reference information for landside disaster mitigation (Žic et al., 2015; Yerro et al., 2016).

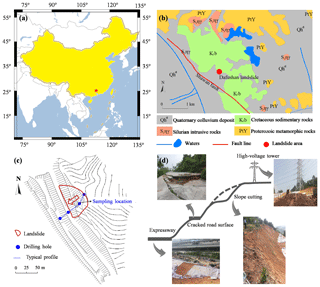
Figure 1 Overview of the Dafushan landslide. (a) Landslide location; (b) geomorphological and geological map of the landslide area; (c) aerial view of the unstable slope; (d) engineering activities on the slope (modified based on Yu et al., 2017, with permission of Springer Nature).

The main numerical methods for simulating landslides are the discrete element methods and the continuum methods (Lu et al., 2014; Wu et al., 2017). Using a discrete element method, such as the distinct element method (DEM) or discontinuous deformation analysis (DDA), the nonphysical parameters cannot be determined exactly (Huang et al., 2014). However, continuum methods based on grids, like the finite element method (FEM) and the finite difference method (FDM), have the shortcomings of grid distortion and low accuracy for the numerical analysis of a landslide with a long runout. Recently, a new numerical method has been used to overcome these limitations, namely the smoothed particle hydrodynamics method (SPH) (Bui et al., 2008). This method is in the framework of continuum methods. SPH is a pure Lagrangian, meshless hydrodynamics method, and it is capable of simulating flow deformation, free surfaces, and deformation boundaries (Liu and Liu, 2003). Several studies have demonstrated the efficiency of the SPH method for the large deformation analysis post landslide. Huang et al. (2014) provided a general view of SPH applications for solving large deformation and failure problems such as dam breaks, slope failure, and soil liquefaction flow. Pastor et al. (2009) applied a depth-integrated, coupled SPH model successfully to simulate catastrophic flow-like landslides that occurred in southern Italy in 1998. Cascini et al. (2014) proposed an SPH model to represent two actual flow-type events accurately. Cuomo et al. (2016) used SPH to simulate flow-like landslides (debris flows and debris avalanches) and discussed the influence of bed entrainment on landslide propagation. Hu et al. (2015) conducted two- and three-dimensional SPH numerical simulations of flow-like landslides triggered by the 2008 Wenchuan earthquake in China and proposed that the SPH method is well suited for modeling free surfaces, moving interfaces, and extensive deformation.

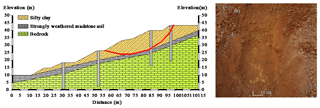
Figure 2 Geology and soil at the Dafushan landslide. (a) Longitudinal geological section of the unstable slope shown in Fig. 1c. (b) Photograph of the silty clay landslide soil.

Study into the residual shear strength property of slip zones under large shear deformation is essential to landslide long-runout mechanism explanations (Tika and Hutchinson, 1999; Wen et al., 2007). Because the physical sample displacement using conventional laboratory shear tests, like direct shear tests and triaxial shear tests, is limited to about 10 mm (Casagli et al., 2006; Okada et al., 2007; Van Asch et al., 2007), the shear behavior for large shear displacements cannot be assessed by these methods (Dai et al., 2016). Ring shear tests, which can impart extremely large shear strains, may be the ideal laboratory tool for extensive shear deformation testing (Okada et al., 2007; ASTM Standard D7608-10, 2010). Several studies have applied ring shear tests to study the residual shear strength of soils (Wang et al., 2005; Fukuoka et al., 2007; Li et al., 2013; Hoyos et al., 2014). For example, Fukuoka et al. (2007) applied a newly developed ring shear test to study shear zone development during large displacements. That study pointed out that a ring shear test is the most appropriate test for studying long-travel landslides. Kimura et al. (2014) studied the effect of the shearing rate on the residual strength of landslide soils using ring shear tests. Zhang et al. (2011) used ring shear tests to study the transform mechanism of the slide–debris flow under large deformations. Li et al. (2017) explored the residual strength of silty sand under different degrees of over consolidations and different shear rates using ring shear tests.

This study presents an effective numerical simulation method, namely SPH, that incorporates accurate soil mechanical parameters derived from ring shear tests. The aim is to predict the downslope flow after slope failure of a previously identified unstable slope and thereby provide basic information for landside disaster mitigation. First, this paper describes the geomorphological and geological setting, hydrogeology and rainfall, and triggering factors of the landslide examined for this case study. These descriptions are based on detailed fieldwork. Next, a series of ring shear tests under several different normal stresses and shear rates were performed to identify the shear strength of the landslide soil. Finally, an SPH-based numerical simulation of the landslide was run to predict the extent of the landslide and track the slide velocity at different times.

2 A case study – the Dafushan landslide

2.1 Geomorphological and geological setting

The Dafushan landslide, located in the Panyu District, Guangzhou city, southern China, was selected for this case study (Fig. 1a). The slope is primarily composed of Cretaceous silty mudstone, conglomerate, and sandstone overlain by Quaternary silty clay (Yu et al., 2017) (Fig. 1b). The landslide is creeping from the northeast to the southwest covering an area of about 70 m × 40 m (Fig. 1c). The height difference between the toe and the crown is approximately 20 m with an average gradient of 25^∘. The Dongxin expressway and a 50 t, high-voltage power line tower are located at the toe and top of the slope, respectively. In addition, there is a fire response service road that runs along the slope that is affected by the slide (Fig. 1d).

Figure 3 Photograph of the GCTS SRS-150 Residual Ring Shear Testing System and an image of the GCTS software interface.

2.2 Landslide triggering factors

The ground was first found to be unstable in May 2013. This instability was manifested mainly by cracks in the ground surface and cracks in the road that lies around the mountain. The road was built for fire response services in May 2011. The relevant departments repaired the damaged road immediately to guarantee the normal operation of the road. However, additional evidence of instability was found in the middle of August 2013 after a period of intense rainfall. The road was damaged again, and the trees up the hill began to tilt. Based on preliminary field investigation, the main factors that triggered the landslide were deduced.

2.2.1 Hydrogeology and rainfall

Rainfall is the main supply source of groundwater in the study area. The average annual rainfall is 1635.6 mm. Most of the rain falls between April and September; this rainfall accounts for 81 % of the yearly precipitation. In the rainy season, the groundwater level rises significantly and reduces the shear strength of the soil. Combined with the rainfall flushing effect on the slope surface, the stability of the slope is decreased significantly.

2.2.2 Mechanical properties of landslide soil

The shallow part of the landslide is mainly composed of silty clay (Fig. 2) and a strongly weathered mudstone soil with a low shear strength. These materials soften and disintegrate when wet; thus, the slope is stable in the dry season but shows signs of instability in the rainy season.

2.2.3 Human engineering activities

Human engineering activities impaired the natural stability of the slope. Two examples include (a) a cut that was made in the slope in order to build the fire service road and (b) the heavy high-voltage power line tower that increases the downward pressure on the slope (Fig. 1d).

3 Ring shear tests

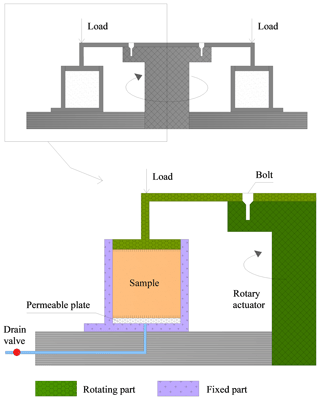
A GCTS Residual Ring Shear Testing System (model SRS-150) produced by Geotechnical Consulting and Testing Systems (GCTS) in 2012 in the USA was used for the ring shear tests conducted for this study (Fig. 3). The SRS-150 is a fully automated electropneumatic and servo-controlled testing system used for determining the residual strength of continuously sheared soil. Shear torques of up to 820 Nm can be applied, consolidation stress can be up to 1000 kPa, and unlimited angular rotation is allowed (Hoyos et al., 2014; Dai et al., 2016). The unit is capable of applying shearing rates of 0.001 to 360^∘ min⁻¹ continuously with zero backlash for replication of true in situ strain rates during failure (Hoyos et al., 2011).

A schematic illustration of a sample in the apparatus is shown in Fig. 4. For testing granular materials, the device accepts ring-shaped samples with a 150 mm outer diameter and a 100 mm inner diameter. The sample is sheared by rotating the upper half of the testing unit and keeping the lower half motionless. Two types of shearing modes, either a shear speed control mode or a shear torque control mode, can be chosen.

Figure 4 Schematic cross sections of the ring shear apparatus shown in Fig. 3.

3.1 Sample preparation and test procedures

The samples studied were samples of the silty clay soil from the Dafushan landslide shown in Fig. 2b. The soil's physical properties are listed in Table 1.

Table 1 Physical properties of a soil from the Dafushan landslide.

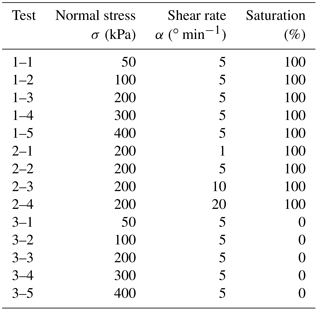
A series of ring shear tests were performed to determine the physical properties of the landslide soil after it had been extensively sheared. The saturated soil sample was first consolidated under normal stress, and then it was sheared to a residual state under naturally drained conditions using the shear speed control mode of the ring shear test system. For these tests, normal stresses of 50, 100, 200, 300, and 400 kPa were used to consolidate the soil samples, and different shear rates (1, 5, 10, 20^∘ min⁻¹) were employed. Test parameters are listed in Table 2.

Table 2 Consolidation stresses, shearing rates, and saturations for soil specimens subjected to laboratory ring shear tests.

Figure 5 Shear stress–angular displacement curves for the landslide soil at a shear rate of 5^∘ min⁻¹ and different axial stresses for (a) saturated soil and (b) dry soil.

3.2 Test results and discussion

3.2.1 Axial stress

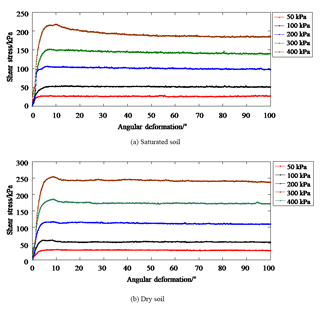
Figure 5 shows the relationships between shear stress and angular displacement under a shear rate of 5^∘ min⁻¹ and axial stresses of 50, 100, 200, 300, and 400 kPa. At the same shear rate, shear strength increases with increasing axial stress. In the initial shear stages, shear stresses increase rapidly along with shear displacement and reach a peak shear strength. The greater the axial stresses, the larger the shear displacement at peak shear strength. When the axial stress is low (e.g., 50 and 100 kPa), the shear stresses do not change after peak shear strength is reached. When the axial stress is high (e.g., 200, 300, or 400 kPa), the shear stresses decrease after peak shear strength but eventually stabilize. This stable strength is the residual shear strength and is the result of strain softening.

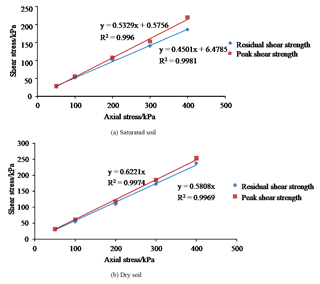
The residual strength envelope of the soil can be illustrated by plotting the shear stress against axial stress, as shown in Fig. 6.

Figure 6 Residual strength envelopes for the landslide soils; (a) saturated soils, (b) dry soils.

Table 3 Cohesion and internal friction for landslide soils at peak and residual shear strengths calculated from the Mohr–Coulomb criterion

Based on the Mohr–Coulomb criterion, the peak and residual shear strengths of the landslide soil were obtained and are listed in Table 3. Because the main trigger for the Dafushan landslide was heavy rain, the residual strength of saturated soil is used for the numerical simulation presented in Sect. 4 of this paper.

3.2.2 Shear rate

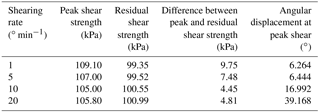
Figure 7 shows the relationships between shear stress and angular deformation under a normal stress of 200 kPa at shear rates of 1, 5, 10, and 20^∘ min⁻¹. As the shear rate increases, the residual shear strengths increase slightly, but the peak shear strengths show the opposite reaction. However, the angular displacements at peak shear strength increase significantly, as shown in Table 4.

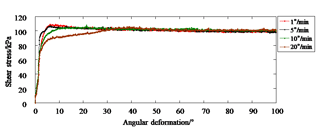
Figure 7 Shear stress–angular displacement curves for saturated landslide soil under 200 kPa axial stress.

Table 4 Differences in shear strengths and angular displacements for saturated landslide soil at different shearing rates.

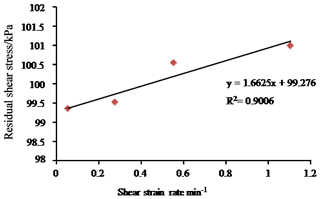
To analyze the relationship between the residual shear strength of the saturated soil and the shear strain rate, the residual shear stress–shear strain rate curve can be drawn (Fig. 8). The formula for calculating the shear strain rate is

$$\begin{array}{}\text{(1)}& {\displaystyle }\dot{\mathit{\gamma }}={\displaystyle \frac{R\mathit{\omega }}{H}},\end{array}$$

where $\dot{\mathit{\gamma }}$ is the shear strain rate, R is the average radius of the sample, ω is the angular velocity, and H is the height of the sample.

As shown in Fig. 8, the residual shear strength of the saturated soil as determined by these experiments increases linearly with shear strain rate. This result agrees with the results reported by Li et al. (2013) and Dai et al. (2016). This relationship is similar to the behavior of a viscous fluid and can be expressed by Eq. (2):

$$\begin{array}{}\text{(2)}& {\displaystyle }\mathit{\tau }=\mathit{\eta }\dot{\mathit{\gamma }}+f\left(\mathit{\sigma }\right),\end{array}$$

where τ is shear stress, and η is the coefficient of viscosity. The intercept f (σ) represents the shear stress when the shear strain rate equals 0.

Figure 8 Residual shear stress–shear strain rate curves for the saturated landslide soil.

Figure 9 Flow chart for the SPH numerical simulation used in this study.

4 SPH-based numerical simulation for landslides

4.1 Calculation principles and SPH process methods

4.1.1 Basic SPH concepts

Smoothed particle hydrodynamics is a mesh-free and fully Lagrangian method based on fluid dynamics. In Lagrangian models, the coordinates move with the medium being modeled. The continuous medium is discretized into a series of arbitrarily distributed discrete elements (called particles), and field variables (like energy, velocity, density, or any other variable) for each particle can be calculated in the form of SPH (Dao et al., 2013; Huang and Dai, 2014).

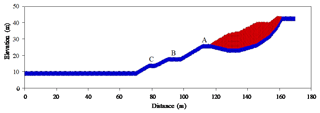
Figure 10 Longitudinal section of the SPH numerical model of the Dafushan landslide. The particles representing the slide mass are shown in red, and the particles representing the fixed boundary are shown in blue.

Figure 11 Predicted results in Dafushan landslide with different calculating parameters.

Table 5 Parameters used in the SPH simulation of the Dafushan landslide.

The SPH method is built on interpolation theory with two essential approximations. These approximations are smoothing and the particle (Huang et al., 2014). The smoothing approximation, also known as kernel approximation, describes a function in a continuous form as an integral representation. The particle approximation means that the value of a function for a particle can be determined by the average value of all the particles in the support domain. The smoothing and the particle approximations can be expressed, respectively, by the following two equations:

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }〈f\left(x\right)〉=\underset{\mathrm{\Omega }}{\int }f\left(x^{\prime }\right)W\left(x-x^{\prime },h\right)\mathrm{d}{x}^{\prime },\text{(4)}& {\displaystyle }& {\displaystyle }〈f\left(x\right)〉=\sum _{j=\mathrm{1}}^N{m}_j{\displaystyle \frac{f_j\left(x^{\prime }\right)}{{\mathit{\rho }}_j}}W\left(x-x^{\prime },h\right),\end{array}$$

where the angle brackets represent a kernel approximation, x is the location vector of the particle, x^′ denotes neighboring particles in the support area, W is the smoothing function, h stands for the smoothing length, Ω stands for the volume of the integral that contains x, m is the mass, ρ is the density, and N is the total number of particles.

4.1.2 Governing equations

The Navier–Stokes equations in a computational fluid dynamics framework are used as governing equations in this study. The equations of continuity and motion in the SPH version can be expressed as

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}{\mathit{\rho }}_i}{\mathrm{d}t}}=\sum _{j=\mathrm{1}}^N{m}_j\left(u_i^{\mathit{\beta }}-u_j^{\mathit{\beta }}\right){\displaystyle \frac{\partial W_{ij}}{\partial x_i^{\mathit{\beta }}}},\text{(6)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}{u}_i^{\mathit{\alpha }}}{\mathrm{d}t}}=\sum _{j=\mathrm{1}}^N{m}_j\left[{\displaystyle \frac{{\mathit{\sigma }}_i^{\mathit{\alpha }\mathit{\beta }}}{{\left({\mathit{\rho }}_i\right)}^{\mathrm{2}}}}+{\displaystyle \frac{{\mathit{\sigma }}_j^{\mathit{\alpha }\mathit{\beta }}}{{\left({\mathit{\rho }}_j\right)}^{\mathrm{2}}}}\right]{\displaystyle \frac{\partial W_{ij}}{\partial x_j^{\mathit{\beta }}}}+F_i,\end{array}$$

where W_ij represents the smoothing function of particle i calculated at particle j, t is time, u denotes the velocity vector, σ is the stress tensor, F represents the vector of external force, and α and β are the coordinate directions.

Table 6 Predicted results in Dafushan landslide with different calculating parameters.

4.1.3 Model for a landslide simulation

The Bingham model has been proven as one of the most effective models for runout simulation of flow-like landslides (Marr et al., 2002; Moriguchi et al., 2009). In this paper, the Bingham flow model is also adopted as the constitutive model for the Dafushan landslide in this study. The relationship between shear stress and strain rate can be written as

$$\begin{array}{}\text{(7)}& {\displaystyle }\mathit{\tau }=\mathit{\eta }\dot{\mathit{\gamma }}+{\mathit{\tau }}_y.\end{array}$$

Equation (7) can be modified by combining it with the Mohr–Coulomb yield criterion (Moriguchi et al., 2009):

$$\begin{array}{}\text{(8)}& {\displaystyle }\mathit{\tau }=\mathit{\eta }\dot{\mathit{\gamma }}+\mathit{\sigma }\tan \mathit{\varphi }+c,\end{array}$$

where τ denotes the shear stress, η and τ_y represent the Bingham yield viscosity and stress, respectively, $\dot{\mathit{\gamma }}$ is the shear strain rate, σ is the pressure, φ is the friction angle, and c is the cohesion.

For this study, the concept of equivalent viscosity was adopted to better integrate the Bingham model into the SPH framework. The equivalent viscosity can be expressed as

$$\begin{array}{}\text{(9)}& {\displaystyle }{\mathit{\eta }}^{\prime }=\mathit{\eta }+{\mathit{\tau }}_y/\dot{\mathit{\gamma }}.\end{array}$$

The maximum value was defined by Uzuoka et al. (1998) as

$$\begin{array}{}\text{(10)}& {\displaystyle }& {\displaystyle }{\mathit{\eta }}^{\prime }={\mathit{\eta }}_{\mathrm{0}}+{\mathit{\tau }}_y/\dot{\mathit{\gamma }}\mathrm{when}{\mathit{\eta }}^{\prime }<{\mathit{\eta }}_{max},\text{(11)}& {\displaystyle }& {\displaystyle }{\mathit{\eta }}^{\prime }={\mathit{\eta }}_{max}\mathrm{when}{\mathit{\eta }}^{\prime }>{\mathit{\eta }}_{max},\end{array}$$

where η_max is the maximum value of η′.

Figure 12 Longitudinal profiles showing the results of the SPH forecasting model. The panels represent the outline of the Dafushan landslide from the time the slide is initiated at t=0 s (a) through the slide finally coming to rest at t=200 s (f).

4.1.4 Procedure for the numerical simulation

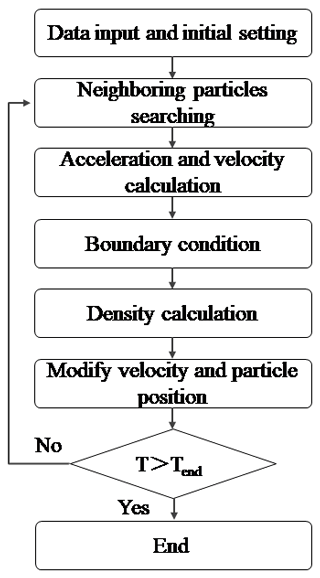
A flow chart for the SPH numerical simulation is shown as Fig. 9. Details about how the calculations are carried out can be found in Huang et al. (2014). The accuracy of the SPH program in landslide modeling was also fully validated in Huang et al. (2014).

Figure 13 Velocity curve of the front and rear edges of the Dafushan landslide as predicted by the SPH model.

4.2 Dafushan landslide SPH simulation and results

Previous studies have been conducted on the verification analysis of landslides, which proves the accuracy of SPH model is relatively high (Huang et al., 2012; Hu et al., 2015). The error of slide distance can reach 4.6 % (Huang et al., 2012). Meanwhile, this study extends the application of the SPH model in combination with accurate soil parameters derived from ring shear tests to predictive analyses of unstable landslides. In addition, two sets of comparative calculations were carried out which demonstrate the robustness of the SPH method.

Based on a terrain model derived from an unmanned aerial vehicle and structure from motion (Yu et al., 2017), an SPH simulation of the failure process of the Dafushan landslide was conducted. Figure 10 is a longitudinal section of the model slide, with the particles in the slide mass shown in red, and the boundary particles shown in blue. The soil particles in the model can be deformed in both the vertical and horizontal directions under gravitational force in the vertical direction.

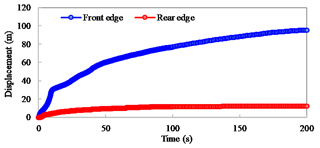
Figure 14 Displacement curve of the front and rear edges of the Dafushan landslide as predicted by the SPH model.

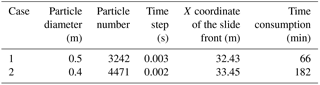
Table 5 lists the parameters used in the SPH simulation of the landslide. The shear strength parameters listed in Table 5, c and φ, are the values calculated from the ring shear tests. Two sets of comparative calculations were conducted as shown in Table 6 and Fig. 11. The parameters of the computer are 3.40 GHz CPU and 16 GB RAM. The results have a high degree of similarity in the slide distance, but the time consumption of case 2, with a particle diameter of 0.4 m and time step of 0.002, is about 2.76 times that of case 1, with a particle diameter of 0.5 m and time step of 0.003. Hence, 3242 particles with diameters of 0.5 m and time steps of 0.003 were applied in our study.

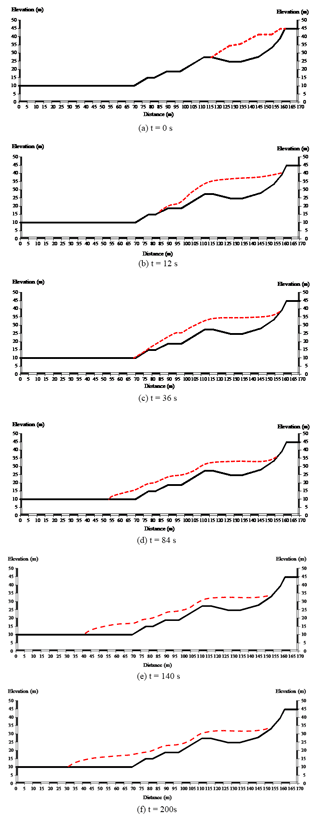
Figures 12a–f show the flow process of the Dafushan landslide predicted by the SPH simulation. In Fig. 12, the solid black line represents the bed on which the mass slides, and the red dashed line represents the SPH-modeled ground surface. At time t=0, this red line is the ground surface before the slide failure. For times after t=0, it is the top surface of the flowing mass of soil that constitutes the moving landslide mass as predicted by the SPH simulation results. In the model, the time the failed Dafushan landslide lasts, from initiation to the whole landslide mass coming to rest, is 200 s. The model predicts that the landslide would cut the fire service road at t=12 s and cover the expressway at t=36 s. When the landslide stops sliding at 200 s, slide material would cover about a 38 m wide swath of ground beyond the foot of the topographic slope.

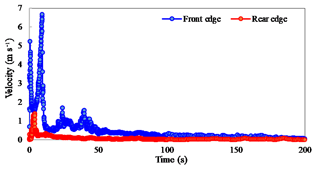
Because this SPH simulation is a Lagrangian method, it can track the velocity and displacement of each particle accurately. The velocity and displacement curves for the front and rear edges of simulated landslide are shown in Figs. 13 and 14. As shown in Fig. 13, the velocity of the front edge increases rapidly after slope failure begins and reaches three velocity peaks as the slide passes the three steps labeled A, B, and C shown in Fig. 10. The speed of the front and the times after initiation that it reaches these three steps are 5.23 m s⁻¹ at 0.6 s at step A, 6.66 m s⁻¹ at 9.3 s at step B, and 1.92 m s⁻¹ at 23.6 s at step C. Unlike the front edge of the landslide, the velocity of the landslide's rear edge shows only a single peak. The maximum speed is 1.40 m s⁻¹; this appears 3.8 s after the slide is initiated.

According to Fig. 14, the maximum flow distances of the front and rear edges are up to 95.4 m and 12.3 m, respectively. The front edge of the slide will destroy the fire service road about 10–12 s after the slide starts and reach the highway at t=36 s. Thereafter, the velocity gradually approaches zero as the flow distance increases. The speed of the front flow can be divided into three stages. The flow of the front edge is fastest from 0 to 10 s, slower from 10–45 s, and slowest from 45 to 200 s. However, once signs of failure are observed at the Dafushan landslide site, evacuation of personnel and vehicles within about 38 m of the slope should begin immediately.

5 Conclusions

In this study, the SPH method incorporating soil mechanical parameters derived from ring shear tests is used to predict the flow of a potential landslide that could develop on an unstable slope in Guangzhou city, China. This study provides basic information for landside disaster mitigation. The conclusions are the following.

1. Under the same shear rate, soil shear strength increases with increasing axial stress. For the conditions used in this study, under high axial stress (> 200 kPa) the soil exhibits strain softening.

2. During ring shear tests, as the shear rate increases, the residual shear strengths increase slightly, but the peak shear strengths decrease as the angular displacements at peak shear strength increase significantly.

3. An SPH-based numerical simulation of the potential Dafushan landslide conducted to predict the scope of the landslide and track the slide velocity at different times shows that the landslide would cut the fire service road at t=12 s and cover the expressway at t=36 s. And once signs of failure are observed at the Dafushan landslide site, evacuation of personnel and vehicles within about 38 m of the slope should begin immediately.