Multi-hazard fragility analysis for fluvial dikes in earthquake- and flood-prone areas

The paper presents a methodology for the multi-hazard fragility analysis of fluvial earthen dikes in earthquake- and flood-prone areas due to liquefaction. The methodology has been applied for the area along the Rhine River reach and adjacent floodplains between the gauges at Andernach and Düsseldorf. Along this domain, the urban areas are partly protected by dikes, which may be prone to failure during exceptional floods and/or earthquakes. The fragility of the earthen dikes is analysed in terms of liquefaction potential, characterized by the factor of safety estimated using the procedure of Seed and Idriss (1971). Uncertainties in the geometrical and geotechnical dike parameters are considered in a Monte Carlo simulation (MCS). Failure probability of the earthen structures is presented in the form of a fragility surface as a function of both seismic hazard and hydrologic/hydraulic load.

1 Introduction

Risk assessment in areas affected by several natural perils can be carried out in two possible ways: on the one hand, one can consider different types of hazards and risks independently, while on the other, possible interactions between hazards can be taken into account. The former approach is based on traditional methods of single-type hazard and risk assessment and represents a common practice. The latter is used much more rarely, as it involves scenarios with obviously lower occurrence probabilities, which might, therefore, be underrated and sometimes unreasonably neglected. At the same time, the tragic lessons of past disasters show that in multi-hazard-prone areas the losses from single hazardous events can dramatically increase due to possible interactions between different types of hazards and the occurrence of cascading effects. For instance, the devastating experience of Hurricane Katrina, 2005, and the Tohoku earthquake followed by a tsunami, 2011, sorely demonstrated that low occurrence probability events may result in extremely significant consequences. Therefore, the possible interactions between hazards in multi-hazard-prone areas should not be ignored in decision-making.

The earlier multi-hazard studies were solely based on the comparison of single-type hazard and risk assessments without considering interactions and potential cascading effects (e.g. HAZUS-MH, 2003; KATARISK, 2003; Grünthal et al., 2006; Fleming et al., 2016). In recent years, frameworks for the assessment of the interactions of multiple hazards have been developed (e.g. Marzocchi et al., 2012; Selva, 2013; Mignan et al., 2014).

The present research work, which was undertaken in the frame of the EU FP7 project MATRIX (New Multi-Hazard and Multi-Risk Assessment Methods for Europe), focuses on the multi-hazard fragility analysis of fluvial earthen dikes or levees. In the presented paper, we develop a methodology for the assessment of fragility due to liquefaction by taking into account potential flood and earthquake impacts on dikes at the Rhine reach around Cologne. The assessment of dike failure probability is a prerequisite for subsequent flood–earthquake multi-risk assessment studies.

The middle Rhine is regularly affected by flooding (e.g. Fink et al., 1996) and vast floodplains are protected by dikes. The areas not protected by dikes are typically behind concrete walls, are safeguarded by mobile flood protection walls or are located on elevated banks.

Besides flood hazard, the areas around Cologne are exposed to other types of natural hazards, in particular windstorms (e.g. Hofherr and Kunz, 2010) and earthquakes (Grünthal et al., 2009; Fleming et al., 2016). Although rarer than floods or windstorms, earthquakes have a higher damage potential (Grünthal et al., 2006; Fleming et al., 2016). In combination with high water levels, an earthquake may lead to liquefaction of saturated earthen dikes.

Dikes may fail due to various failure mechanisms induced either by high water levels and/or earthquake impact (Armbruster-Veneti, 1999; Foster et al., 2000; Apel et al., 2004; Allsop et al., 2007; Briaud et al., 2008; Wolff, 2008; Van Baars and Van Kempen, 2009; Vorogushyn et al., 2009; Nagy, 2012; Huang et al., 2014). When considering solely hydrologic/hydraulic load, overtopping is the most common failure mechanism followed by piping and slope instability (see Vorogushyn et al., 2009 and references therein). For these breach mechanisms, approaches for fragility analyses have been proposed (Apel et al., 2004; Vorogushyn et al., 2009). Under earthquake load, the liquefaction phenomenon is indicated as the most important cause of dike failure (Ozkan, 1998).

Marcuson et al. (2007) reviewed the development of the state of practice in seismic design and analysis of embankment dams or dikes, starting from the fundamental publications of Newmark (1965) and Seed and Idriss (1971). Sasaki et al. (2004) described empirical and analytical methods used in Japan for estimating the settlement of dikes due to liquefaction, considering both the probable subsidence of the bottom boundary and deformation of the dikes. Singh and Roy (2009) proposed a correlation relationship for the earthquake-induced deformation of earthen embankments based on the examination of 156 published case histories and using the ratio of the peak horizontal ground acceleration and the yield acceleration as an estimator.

In recent years, more sophisticated computer-based linear or non-linear methods for seismic analyses of embankments have been developed, using one-, two- (Kishida et al., 2009; Athanasopoulos-Zekkos and Seed, 2013) or three-dimensional (Wang et al., 2013) models. At the same time, Kishida et al. (2009) concluded that simplified models based on equivalent linear analyses can provide reasonably accurate results up to moderate ground shaking levels, while nonlinear analyses should be used to evaluate dike responses at stronger shaking levels. We therefore focus on a simplified approach, since we are concerned with the study on a regional spatial scale in areas of low to moderate seismicity.

Rosidi (2007) presented a seismic risk assessment procedure for earthen levees, whereby dike fragility was expressed as a function of earthquake-induced slope deformations. Considering different strengthening scenarios, Rosidi (2007) estimated levee failure probabilities depending on earthquake ground motion return period. However, possible fragility changes due to floodwater elevation and dike core soil saturation was not taken into account in that study.

For the purpose of single-type flood risk assessment, Apel et al. (2004) developed fragility curves for overtopping failure based on Monte Carlo simulations. Vorogushyn et al. (2009) extended this approach for piping and micro-instability breach mechanisms based on the formulations of Sellmeijer (1989) and Vrouwenvelder and Wubs (1985), respectively.

Recently, Schweckendiek et al. (2014) presented an approach to include field observations in the Bayesian updating of piping failure probabilities of dikes in the Netherlands. Krzhizhanovskaya et al. (2011) reported an integration of reliability analysis for various breach mechanisms into a prototype flood early warning system, including dike failure and associated inundation modelling. A summary of research and practical methods for reliability assessment of levee systems considering different failure mechanisms can be found in Wolff (2008).

The reviewed studies, however, used a single-hazard approach focusing on either earthquake or flood impacts on infrastructure. The present study aims at filling the existing methodological gap considering both hazards together. The main goal of the study is the development of a methodological approach for multi-hazard fragility analyses and construction of multi-hazard fragility functions for dikes in the earthquake- and flood-prone areas along the Rhine River. Extending the previous studies, we consider here another possible failure mechanism – earthquake-triggered physical damage to earthen dikes due to liquefaction. This type of phenomenon may occur in earthquake-prone areas, where water-saturated sandy soils have the potential to liquefy when subjected to seismic vibrations. Fragility functions are meant to be incorporated into the regional flood hazard and risk assessment models (e.g. Vorogushyn et al., 2010). In this way, small-scale breaching process knowledge (e.g. Rifai et al., 2017) can be integrated into regional-scale risk analyses. These analyses go beyond the scope of the presented paper and will be elaborated in a following study.

2 Data and method

The area under study, the communities at risk and the location of dikes along the Rhine River are presented in Fig. 1, where the points correspond to the geometric centres of the dike sections of about 500–600 m length. Figure 1 shows the administrative boundaries (communities) as well as the general zonation of the seismic hazard. The depicted hazard estimates are based on the earlier map by Grünthal et al. (1998) in terms of European macroseismic scale (EMS) intensities for an exceedance probability of 10 % in 50 years, and refer to the centres of communities (Tyagunov et al., 2006a). The accurate seismic hazard estimates for all dikes locations will be calculated below.

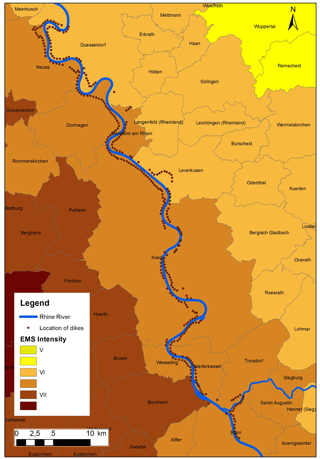
Figure 1 Location of flood protection dikes along the Rhine and the spatial distribution of seismic hazard in the study area in terms of EMS intensities for an exceedance probability of 10 % in 50 years (Grünthal et al., 1998).

During liquefaction, when, because of increased porewater pressure, the strength of bonds between soil particles is drastically reduced to essentially zero, soil deposits may lose their bearing capacity and behave as fluids (Kramer, 1996; Idriss and Boulanger, 2008). In our study, we assume that the liquefaction occurrence in the dike body may result in the subsidence of the core as well as in large slope deformations. The subsequent breach of the affected dike section is the resulting consequence.

The probability of a dike failure is considered in terms of liquefaction potential, estimated using the method of Seed and Idriss (1971). The liquefaction potential can be assessed with a factor of safety (FS) against liquefaction, which is determined as the ratio of the capacity of the soil to resist liquefaction (CRR, cyclic resistance ratio) and the seismic demand placed on the soil layer (CSR, cyclic stress ratio).

The CSR value can be estimated using the following expression:

$$\begin{array}{}\text{(1)}& \text{CSR}=\mathrm{0.65}\times {\displaystyle \frac{a_{\text{max}}}{g}}\times {\displaystyle \frac{{\mathit{\sigma }}_{\text{vo}}}{{{\mathit{\sigma }}^{\prime }}_{\text{vo}}}}\times r_{\text{d}},\end{array}$$

where a_max is the horizontal peak ground acceleration (PGA), g is the gravitational acceleration, σ_vo and ${{\mathit{\sigma }}^{\prime }}_{\text{vo}}$ are the total and effective overburden stresses (pressure imposed by above layers) of the soil, respectively, and r_d is a stress reduction factor that depends on the depth. For the calculation of the vertical stresses as a function of depth, we also consider the variations in the water level in the river, which influences the phreatic surface and degree of saturation in the dike core.

As for the CRR value, there are different methods for estimating the soil resistance to liquefaction (Youd et al., 2001; Kramer and Mayfield, 2007). Probably the most common is the method based on standard penetration testing (SPT). In our study, due to the lack of SPT data, we use an approach based on the correlation between penetration resistance and the angle of internal friction for sandy soils (Table 1, Peck, 1974).

Table 1 Relationship between the angle of internal friction and SPT values (Peck, 1974).

In addition to the friction angle, for modelling the bearing capacity of earthen dikes, we also consider other geotechnical parameters such as specific weight, porosity and fines content. Statistical information about the characteristics of dikes used for liquefaction analysis is presented in Table 2. The typical values for the specific weight and friction angle found in dikes were taken from Vorogushyn et al. (2009) and the references therein. The fines content values are adapted from a dike at the Rhine River in the Netherlands (Alexander Van Duinen, personal communication, 2013).

Table 2 Geotechnical parameters of dikes adopted in this study.

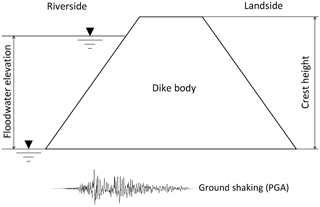
The performance of dikes under seismic ground motion loading is analysed using a simplified one-dimensional model assuming that below the water level the soil is in a saturated state. Hence, the phreatic line within the dike body is assumed to be horizontal (obviously, this is a conservative assumption that presumes the sufficiently long duration of the floodwater rise or impoundment). A cross-section of the generic dike model is shown in Fig. 2.

Figure 2 Generic dike model to illustrate the earthquake–flood–dike interaction.

For the development of dike fragility curves, we assume a generic dike height of 5 m. When integrated into the dynamic flood–earthquake hazard model, the actual dike height and corresponding water level need to be taken into account.

In the computational algorithm, the material properties of dikes are assumed to be homogeneously distributed throughout the cross-section of the dike core. However, they can vary spatially along the river, from one cross-section to another, keeping in mind the range of existing uncertainties of the geotechnical parameters as specified in Table 2.

For quantifying the liquefaction potential, the values of CSR (reflecting the level of seismic ground shaking) and CRR (depending on the dike material properties and the water level) are calculated for all points of the dike cross-section from the crest to the bottom (with a discretization interval of 5 cm). Once both the CSR and CRR values have been determined at a certain point under certain load conditions, we can calculate the factor of safety (FS) against liquefaction employing the following relationship (Seed and Idriss, 1971):

$$\begin{array}{}\text{(2)}& \text{FS}={\displaystyle \frac{\text{CRR}}{\text{CSR}}}.\end{array}$$

At the points where the loading (CSR) exceeds the resistance (CRR), i.e. the factor of safety is below 1, one can expect the initiation of liquefaction that can lead to functional failure. In this study, we neither analyse the degree of soil deformations caused by liquefaction nor consider the variety of possible failure states of the affected structure. Instead, we conservatively assume that the initiation of liquefaction (FS ≤ 1) at any point throughout the dike body corresponds to the failure (loss of function) of the dike.

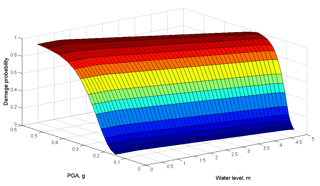
Computations of the liquefaction potential are done in a Monte Carlo simulation (MCS) considering the variability (uncertainty) of the geotechnical parameters of the dikes (Table 2). Based on a frequency analysis of the MCS results, dike failure probabilities are computed for different points of the discretized two-dimensional load space, considering possible combinations of peak ground acceleration and floodwater level.

3 Fragility surface

In the single hazard fragility analysis, the failure probability is expressed as a function of single hazard load parameter(s). In a multi-hazard fragility analysis the response of the structure is described as a function of multi-hazard load parameters. Thus, in our case the calculated fragility results are presented in a three-dimensional form, with seismic and hydraulic load described by peak ground acceleration and water level, respectively (Fig. 3). The fragility surface represents the conditional failure probability given the combination of load.

Figure 3 Multi-hazard fragility surface for liquefaction failure of a dike.

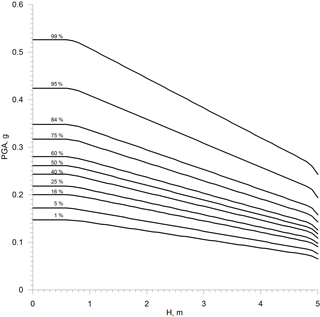
The fragility surface can be interpreted as a set of isolines corresponding to different percentiles of the calculated distribution of the FS values, as shown in Fig. 4. The presented isolines correspond to the occurrence of the limit state (FS = 1) and specify the failure probabilities in the two-dimensional space of hazards (in units of PGA and floodwater level).

Figure 4 Dike failure probability in the PGA and water level space.

It becomes apparent that liquefaction failure can already be initiated at small water levels given sufficient earthquake load. On the other hand, a certain degree of shaking is required for liquefaction failure, even at the maximum water levels (Fig. 4). The estimated PGA threshold ranges from 0.15 to 0.54 g for the interval from 1 to 99 percentiles. When the floodwater rises up to about 0.7–0.8 m, it has no visible effect on the PGA threshold, while further increases in water levels lead to a considerable shift towards lower PGA values, and this change is linear. When the water level reaches the top of the structure, the threshold PGA values and the liquefaction occurrence probabilities change significantly. In comparison with the initial state (water level at the toe of the dike), the PGA threshold values decrease to between 0.07 and 0.24 g (for the interval from 1 to 99 percentiles). Comparing the two extreme cases, the liquefaction-triggering PGA threshold values decrease by more than half and the spread of the values becomes narrower. Water level is thus a considerable factor determining the dike core moisture content and liquefaction failure.

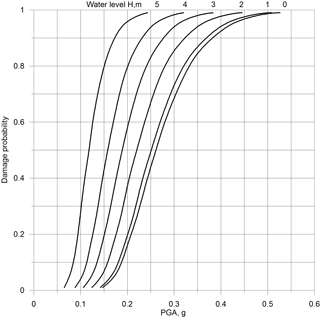
Figure 5 Fragility functions for earthen dikes for different water levels ranging from the dike toe to the assumed crest height.

The developed dike fragility model may find practical application in regions of low to moderate seismicity. For the lower PGA values (0.15–0.30 g) the contribution of the effect of impoundment can be more critical than for the higher PGA, when earthquake ground shaking is sufficiently strong to trigger liquefaction under conditions without extra flooding (Fig. 5). It should be stressed here that the presented fragility curves represent conservative estimates due to the assumption of full saturation of a dike core below the water level. In practice, some time is however required for the development of the phreatic line. More sophisticated dynamic models considering the degree of soil saturation can be adapted in future to adjust failure probability estimates.

4 Dike failure probability assessment

To estimate the actual failure probability of a dike in the area of interest, the developed multi-hazard fragility functions should be combined with the probabilistic hazard estimates of earthquake and flood considering their respective return period values.

The developed fragility curves are intended to be used in a subsequent multi-risk analysis study along the Rhine River reach between Andernach (Rhine-km 613.8) and Düsseldorf (Rhine-km 744.2) considering flood scenarios with return periods between 20 and 1000 years. In particular, the effect of multi-hazards is expected to manifest for flood return periods below the dike design level (200-year return period on the middle Rhine). In the single-type flood hazard analysis, only piping failure could possibly impact dikes below design level, whereas multi-hazard consideration would slightly increase the probability of failure if the occurrence of earthquakes and subsequent liquefaction is taken into account. The effect of multi-hazard consideration on total risk is expected to decrease with increasing flood return period beyond the design level since dikes would fail (in most cases) due to overtopping anyway. A full multi-risk assessment considering dike failures among others due to liquefaction is beyond the scope of the presented study. Hereafter, we illustrate a framework for how to integrate seismic and hydraulic load for the calculation of the multi-hazard failure probability and demonstrate this with one example of a selected dike section.

The seismic hazard calculations were accomplished for all locations at the centre points of dike segments on both sides of the Rhine River reach (Fig. 1). The input data for the seismic hazard analyses were taken in accordance with the regional model of Grünthal et al. (2010). The hazard calculations were carried out using the GEM (Global Earthquake Model) OpenQuake software (Crowley et al., 2011a, b) for soil sites characterized by 300 m s⁻¹ shear wave (S wave) velocity in the uppermost 30 m, which was assigned considering the results of previous seismological studies in the area (Tyagunov et al., 2006b; Parolai et al., 2007). Note that amongst the waves generated by an earthquake, the S waves, that is, those for which the motion is perpendicular to the direction of wave propagation, are expected to determine the largest impact on the building structures. Their variations in the velocity of propagation, accounted for in the calculation, are used as a proxy to estimate the spatial differences in the amplitude of shaking. The set of calculated seismic hazard curves, which in terms of PGA characterize the range of probable levels of ground shaking for the different dike locations, is shown in Fig. 6. In total, 339 dike sections are analysed: 157 of them are on the left side and 182 on the right side of the river.

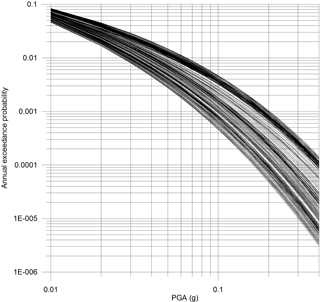
Figure 6 Seismic hazard (mean) curves for the locations of the dikes along the Rhine River. Each curve corresponds to one dike segment.

The calculated PGA values vary in space for different points along the river stretch, and the level of ground shaking depends on the return period of interest. Thus, for the level of exceedance probability of 10 % in 50 years, which is the common standard in the practice of earthquake engineering and corresponds to an average return period of 475 years, the PGA estimates vary over a range of about 0.06–0.15 g. For a shorter return period of 100 years, PGA varies in the range of about 0.03–0.06 g, whereas for a longer return period of 1000 years, the range is about 0.08–0.20 g. Note, however, that for return periods longer than 1000 years, even higher levels of ground shaking are probable in the area and such low probability phenomena cannot be ruled out.

The spread in the calculated PGA values is not very large because the course of the Rhine River and corresponding dikes closely follows the shape of the seismic hazard zones around Cologne (Grünthal et al., 1998; DIN 4149, 2005). Therefore, the seismic hazard distribution in the area under study (Fig. 1) appears to be rather uniform.

Based on the obtained results and referring to the liquefaction susceptibility categorization for different soil types (Youd and Perkins, 1978; HAZUS-MH, 2003), one can make a qualitative conclusion that in this area, there is a risk of dike failure due to liquefaction induced by seismic ground shaking. According to observations from past earthquakes (Sasaki et al., 2004) seismic impact on river dikes can be triggered by a PGA of 0.16 g or higher. There is even evidence that the PGA threshold for liquefaction occurrence can be even less than 0.10 g (Santucci de Magistries et al., 2013; Quigley et al., 2013).

The actual dike failure probabilities can be quantified by considering the probabilities of occurrence of the earthquake ground shaking level and flood return periods at different dike locations combined with the presented fragility curves. The simultaneous occurrence of a flood and an earthquake should be assumed. The typical duration of a flood wave of 30 days is considered for the Rhine. It is assumed that no dike repair actions are undertaken in this period, which may affect the probability of failure. Thus, the earthquake probability is computed for this period to be combined in the following expression to determine the actual failure probability:

$$\begin{array}{}\text{(3)}& P\left(F\right)=\int \int P\left(F\right|S_i^{\mathrm{30}},W_j)\times P(S_i^{\mathrm{30}})\times P(W_j)\text{d}S\text{d}W,\end{array}$$

where $P\left(F|S_i^{\mathrm{30}},W_j\right)$ is the conditional failure probability given the combination of the seismic ground shaking $S_i^{\mathrm{30}}$ within a time window of 30 days and the water level W_j; $P\left(S_i^{\mathrm{30}}\right)$ is the probability of occurrence of the seismic input S (peak ground acceleration) of the level i within a time window of 30 days; P(W_j) is the probability that the water level W corresponds to the level j.

The first factor in the integral represents the conditional failure probabilities, which can be obtained from the multi-hazard fragility surface (Fig. 3), while the second and third ones represent probabilistic estimates of the seismic (PGA level) and flood hazard (water level) at the dike locations and can be obtained from the corresponding hazard curves.

For the situation without flooding by combining the seismic hazard curves (Fig. 6) with the fragility curve corresponding to the water level of 0 m (Fig. 5), the earthquake-triggered liquefaction may occur at some of the considered dike locations, though the probability is not very high. The probability varies in this case within the range of 1–$\mathrm{4}\times {\mathrm{10}}^{-\mathrm{5}}$ per year.

The current design criteria of fluvial dikes only take into account flood hazard and do not consider potential multi-hazard impact. Therefore, in the case of potential temporal coincidence of flooding and strong earthquakes, dike protection structures may fail due to liquefaction for flood return periods below the design level. This may lead to perplexity and negatively affect population, infrastructure and flood response, requiring emergency actions.

A comprehensive quantitative risk analysis considering the joint probability of seismic and flood events and their interactions in time and space requires continuous hydraulic model and multi-hazard integration. This goes beyond the scope of the presented research and will be a subject of a subsequent study. Here, for illustration purposes, we present an example for estimation of the failure probability for a specific dike section considering previously computed seismic and hydraulic load.

For a left-side dike section at Rhine-km 668 near the town of Wesseling (south of the city of Cologne; Fig. 1), the average maximum water levels were estimated for three return periods, 200, 500 and 1000 years, using a dynamic probabilistic–deterministic coupled one-dimensional–two-dimensional model (Vorogushyn et al., 2010) set-up for the study area at the Rhine River within the EU-FP7 MATRIX project (Garcia-Aristizabal and Marzocchi, 2013). The hydraulic model uses the flow records at the gauge at Andernach (Rhine-km 613.8) for the estimation of hydrographs and corresponding return periods. Hydrographs are then routed with a coupled one-dimensional–two-dimensional model considering dike breaches and associated inundation. The estimated water levels at the selected location are 50.38 m.a.s.l. for the 200-year return period (p=0.005 per year) and 50.49 and 50.52 m.a.s.l. for the 500-year (p=0.002) and 1000-year periods (p=0.001), correspondingly.

Assuming the height of the dike of 5 m at the selected location, the dike would be impounded by 4.50 m during a 200-year flood event. Correspondingly, the estimated impoundment level would reach 4.61 m for the 500-year and 4.64 m for the 1000-year flood scenarios. The small difference between the calculated estimates can be explained, in particular, by the model used, which considers dike breaches upstream; i.e. the water level at one dike location depends on the performance of other dike sections (e.g. if one of the upstream dikes fails, the water outflow would reduce the flood loads on the other dike sections).

Combining the flood hazard estimates with seismic hazard curves and fragility function for the point of interest, the probability of liquefaction at Wesseling without flooding is about $\mathrm{3.9}\times {\mathrm{10}}^{-\mathrm{5}}$ per year. Applying Eq. (3), we obtain the liquefaction failure probability of 1 10⁻⁶ per year for the 200-year flood scenario, about $\mathrm{4.1}\times {\mathrm{10}}^{-\mathrm{7}}$ per year for the 500-year flood and about $\mathrm{2.1}\times {\mathrm{10}}^{-\mathrm{7}}$ per year for the 1000-year flood. All these return period scenarios contribute to the total risk value. Consequently, it is expected that the multi-hazard interaction scenarios essentially increase the total risk level in comparison with the estimated single hazard risk level, though the combined probabilities of earthquake and floods are very small.

Nevertheless, dike failures due to liquefaction in the case of a multi-hazard impact bear the potential of surprise and malign consequences, which should be considered in a comprehensive risk assessment (Merz et al., 2015). In particular, under hydraulic load below the (hydraulic) design level (<200-year return period at the German Rhine reach), dikes might be considered predominantly safe in a single-type hazard analysis, whereas the occurrence of liquefaction would dramatically change flood inundation patterns and loss distribution. Though not necessarily extreme, but still significantly strong, floods and “unexpected” dike failures in combination may still harmfully affect the densely populated areas with high asset concentration, such as the floodplains along the Rhine. Hence, a quantitative multi-risk analysis is advocated in earthquake- and flood-prone areas considering the effect of dike liquefaction despite a relatively small probability of the joint occurrence of both perils.

5 Conclusions

A methodology for multi-hazard fragility and failure probability analyses of fluvial dikes in earthquake- and flood-prone areas is presented. The failure probability is described by a three-dimensional fragility surface as a function of both earthquake ground shaking (PGA) and floodwater level (impoundment of the dike). Quantitative fragility analysis shows that a rise in floodwater level reduces the liquefaction-triggering PGA threshold due to high moisture content in the dike core. When considering earthquake and flood hazard and the developed fragility curves, the non-zero liquefaction probability for an exemplary dike location becomes evident.

A framework for the multi-hazard calculation of dike failure probability due to seismic shaking and hydraulic load was presented and exemplified for the flood protection dikes along the Rhine River in the area around Cologne. Though the probability of joint occurrence of both perils is rather low, we argue that such incidents bear a high potential of surprise with substantial negative consequences. The latter can be, however, avoided by multi-risk considerations and awareness of civil protection authorities and among the public.

The developed fragility curves for liquefaction will be used for a comprehensive multi-risk assessment study along the Rhine River in a subsequent work. This will take the interaction of earthquake and flood hazards, dynamic inundation effects and damage modelling into account.